拉格朗日对偶问题

拉格朗日乘数法

要理解拉格朗日对偶问题，就必须先理解什么是拉格朗日乘数法。

拉格朗日乘数法的几何意义

为此，我们考虑这样的一道题：

那么我们按照书上的定义，一般会按照如下的流程来解决这个问题

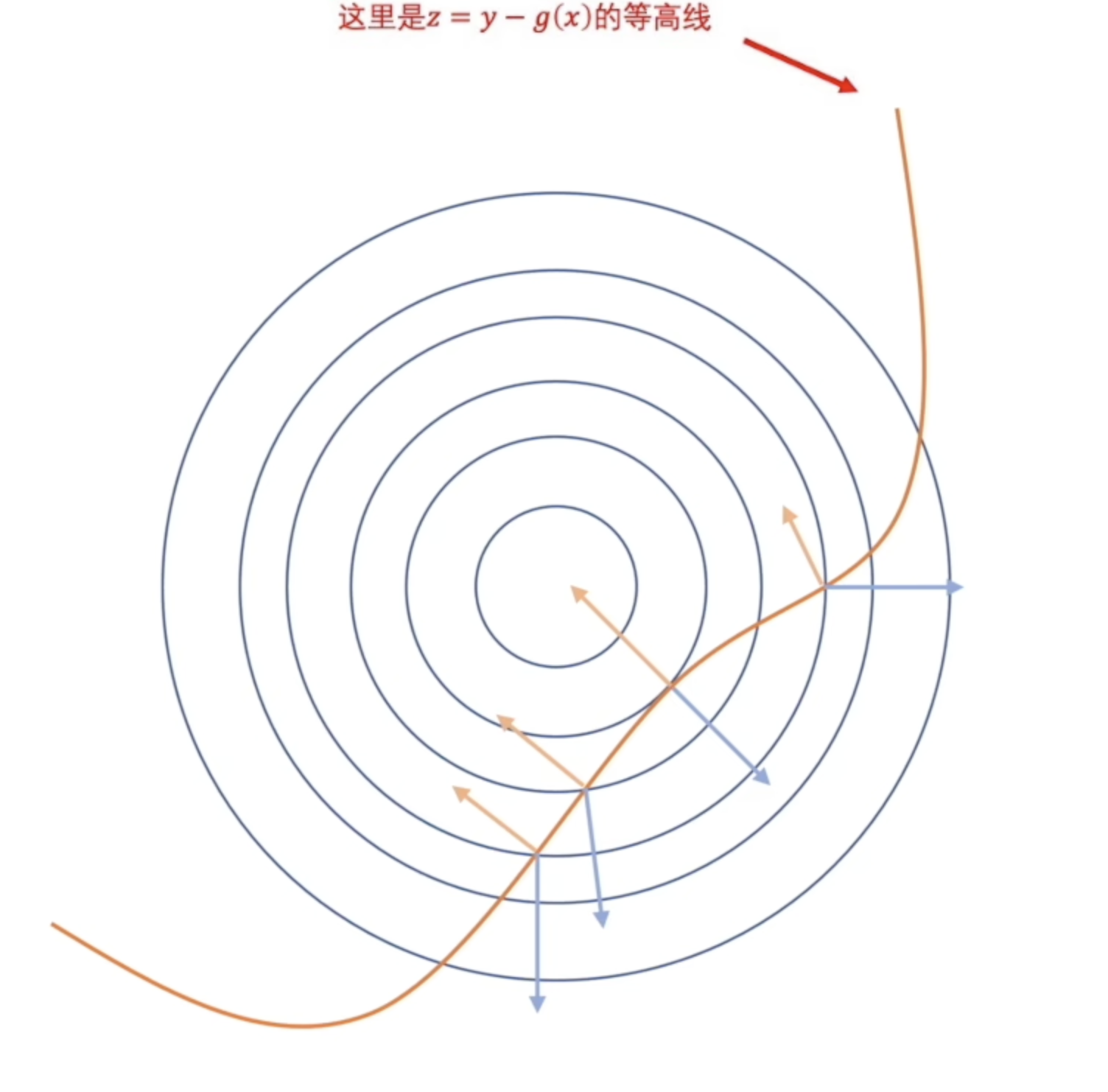同样的，我们也可以按照几何意义的方式来理解。很显然的，为了让梯度为0，我们必须让的梯度和的梯度大小相等，方向相反。

对于约束条件更复杂的情况，我们可以这样理解：
比如这样的一个题目：

我们可以得到其拉格朗日乘数法的方程为：

我们让梯度为0可以得到


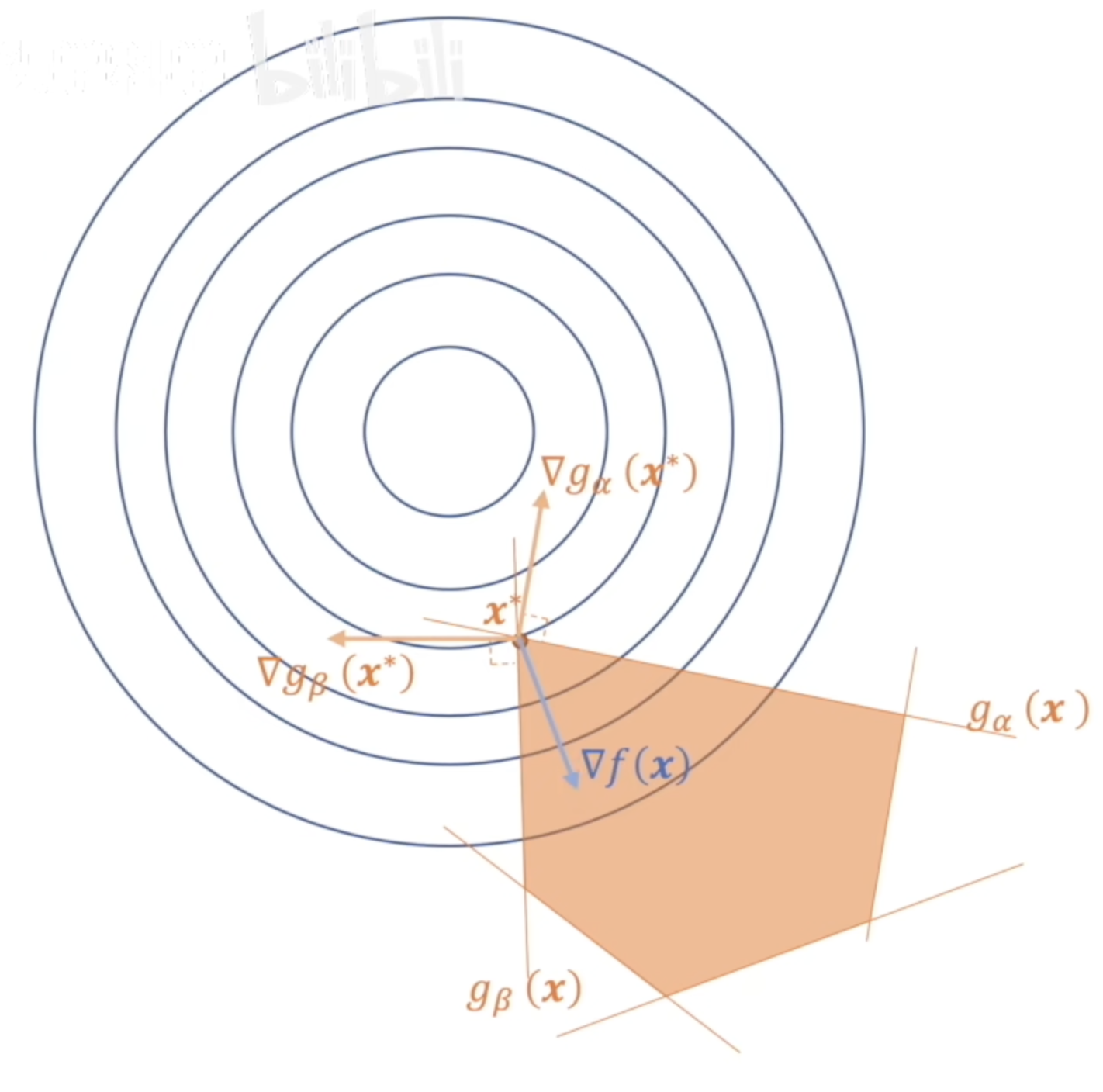
也即上图的样子。
橙色阴影部分即为可行域。我们一眼便能看出其解的位置，我们设极值点为。
那么，我们可以注意到：

前一个是显然的，因为解同时在两条直线上，那么只能等于0.
后面一个并不显然，只能从图像理解，我们可以理解为是只有这两个梯度起作用了，因为其他的梯度都没限制到极值点。因此只有这两个梯度能够对梯度进行限制。
基于此，我们可以推出：
其他，
，即非那两个限制约束的梯度之外，其余的lambda全部为0。
因此，我们可以推导出这样的一个式子
所有
这里的松弛和紧致的意思，更严格的可以理解为：极值点是否在边界上。
这个式子就是后面的松弛互补条件的理解。

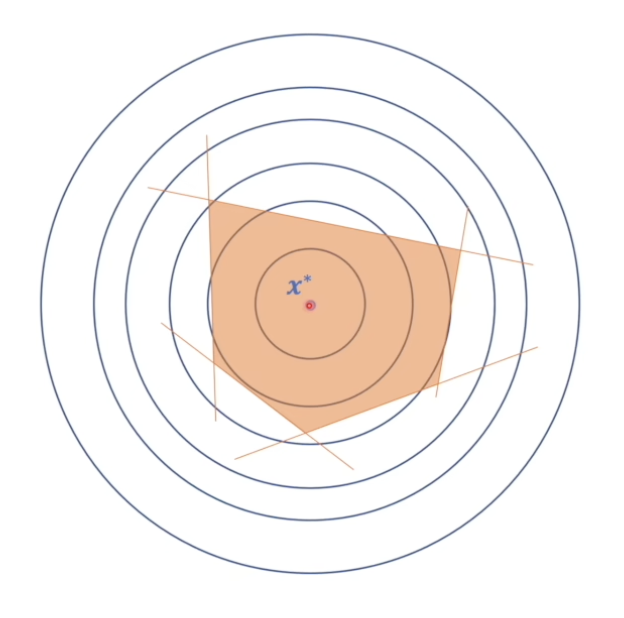
对于这种情况，极值点本身就在可行域范围之内的，我们认为所有的约束条件都是松弛的。即所有的都为0

拉格朗日乘数法的变换

考虑这样的一个问题：
我们便可以将其变换为这样的问题：

理由如下：
由于在确定max之后，还需要确定min，因此该问题和原问题等价。

拉格朗日乘数法的局限性

主要问题是，它求出的极值点并不一定是最值点。想要满足极值点=最值点的话，那么求解的函数就必须是一个凸函数才行。

拉格朗日对偶问题

对于刚刚上面的这道题，我们可以把它的对偶问题写出来：

容易发现，就只是max和min交换了一下顺序而已。

为什么要用对偶问题？
就是为了解决拉格朗日乘数法的局限性，凡转化为拉格朗日对偶问题，他都一定是一个凸问题。

凸的定义

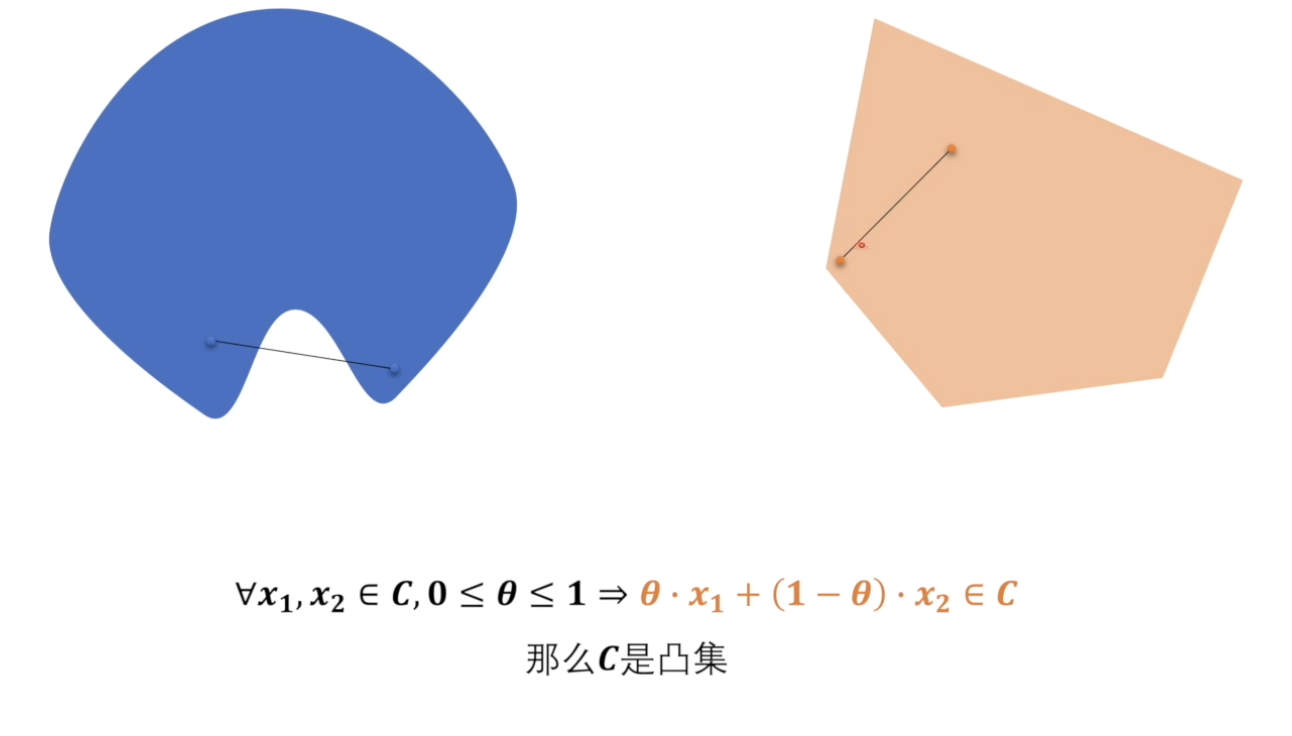
凸集

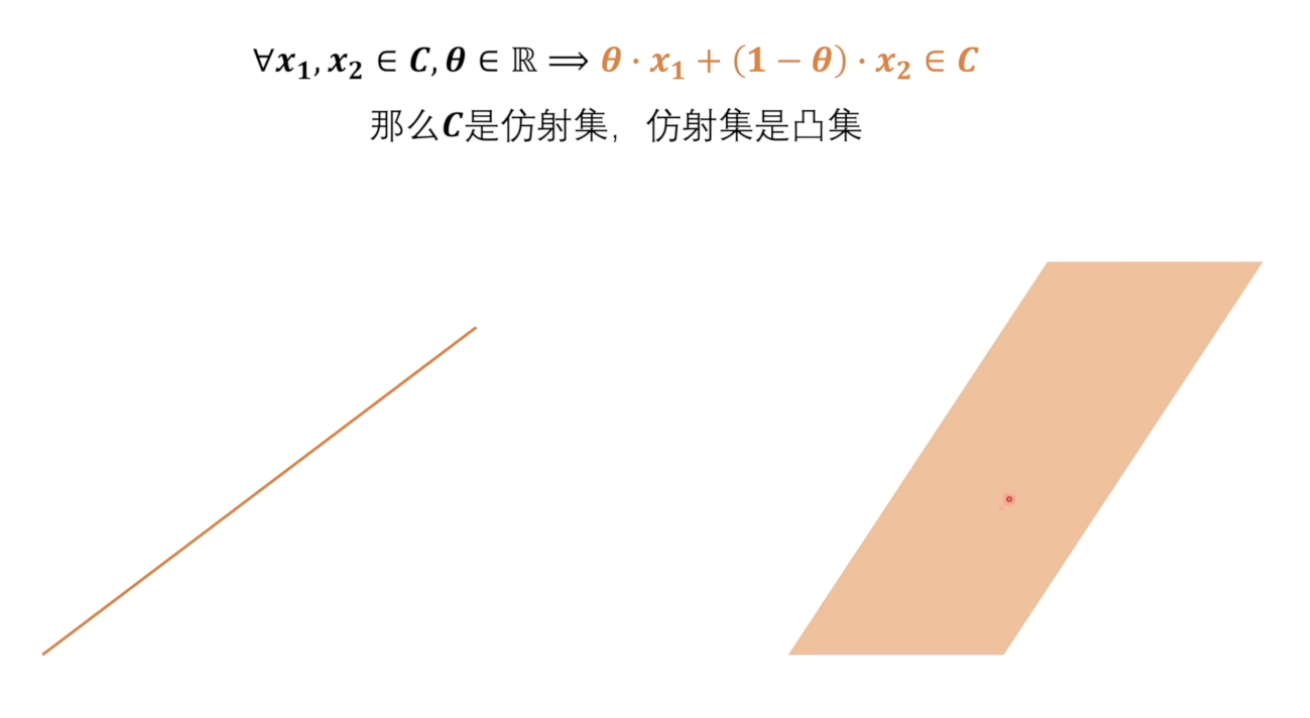
注意，仿射集的交际，也是凸集


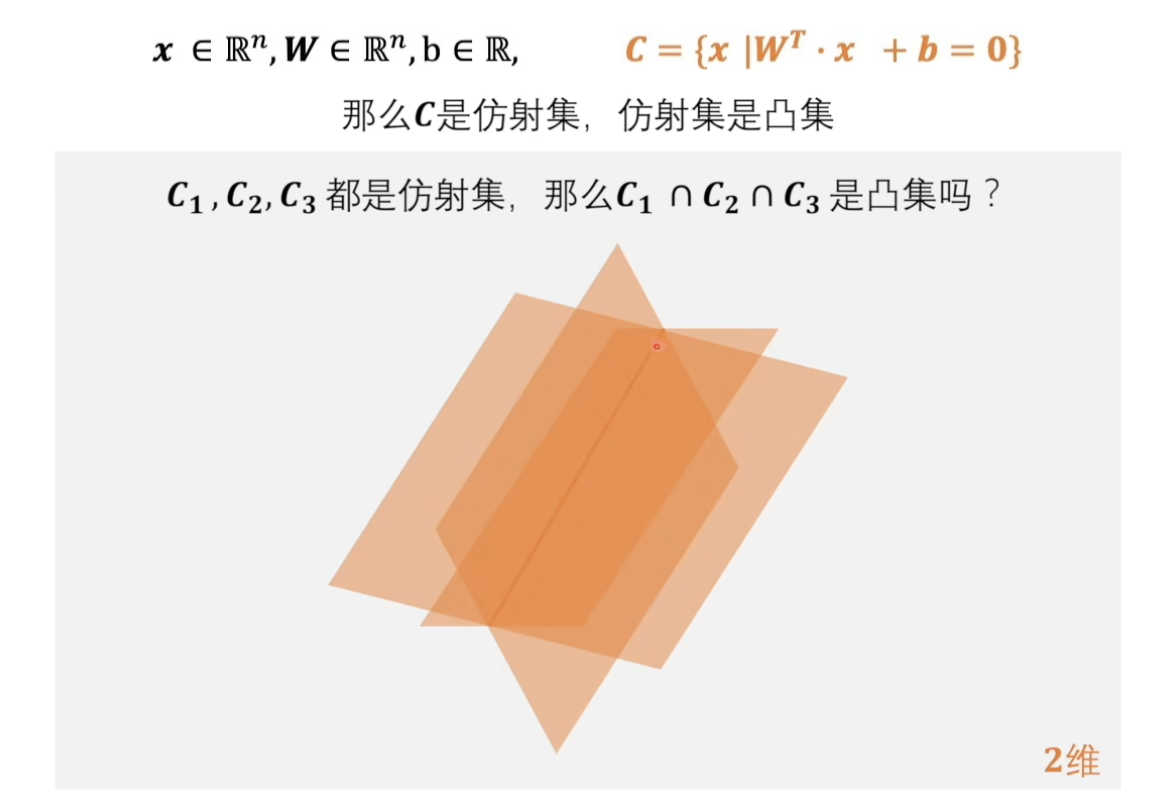
同仿射集，半空间的交集也一定是凸集。

凹函数和凸函数

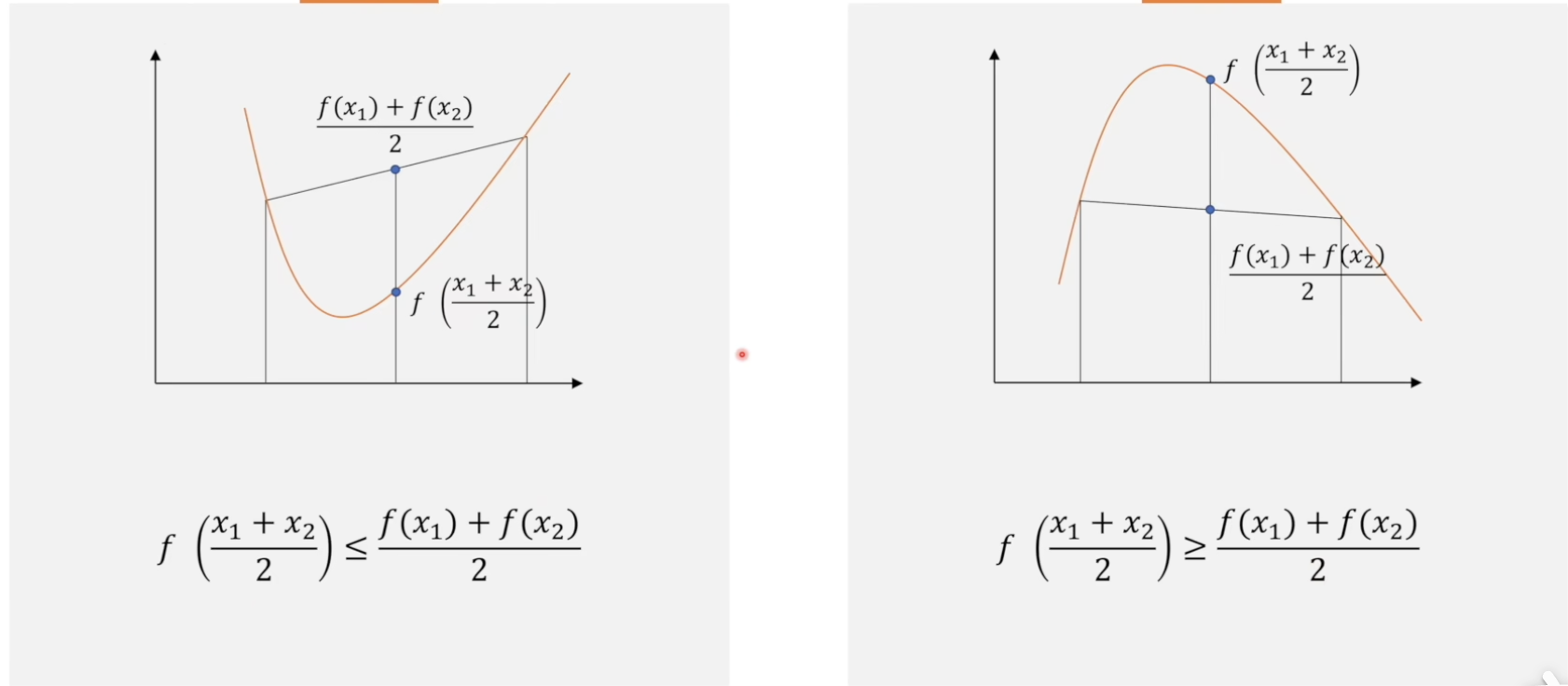
这里左边是凸函数，右边是凹函数

分析对偶问题的凸性

首先我们给出对偶函数
要求原问题，就是要求
那么，我们先分析对偶函数。
我们假设是使得对偶函数最小的那个点，那么我们有

在这个式子中，都是常数，可以忽略
那么这个对偶函数，其实就是一条直线。对于一条直线来说，他可以是凸函数也可以是凹函数。那么这里我们求的是max，因此我们就让他是凹函数。
对于约束条件，我们可以把它看作是一个半空间，因此这里的可行域也是一个凸集。

综上，因为对偶问题的对偶函数是凸函数，对偶问题的可行域是凸集，因此对偶问题一定是一个凸优化问题。

原问题和对偶问题的等价条件

首先先给出一个结论，原问题的解，一定是大于等于对偶问题的。
下面进行证明：其中是原问题的解，是对偶问题的解。

接下来，我们给出取等的条件
为了方便理解，我们用几何的方式来说明

首先对拉格朗日乘数的式子进行简化

根据约束条件，由于这里不用求梯度，因此可以直接省去最后一项，转化为我们让, ，因此原式可以化简为
我们把t和u看成是两个变量，将其映射到坐标轴上。

对于原问题(没有经过乘数法变换形式)，我们的可行域是：
其中
因此原问题的解空间是：

对于拉格朗日对偶问题，我们的可行域是
因此，对偶问题的解空间是：

容易注意到，G1和G2之间的差距仅仅在于x的取值范围上。那么G1一定是G2空间中的一部分。
因此，我们可以这样画出两个问题的解空间

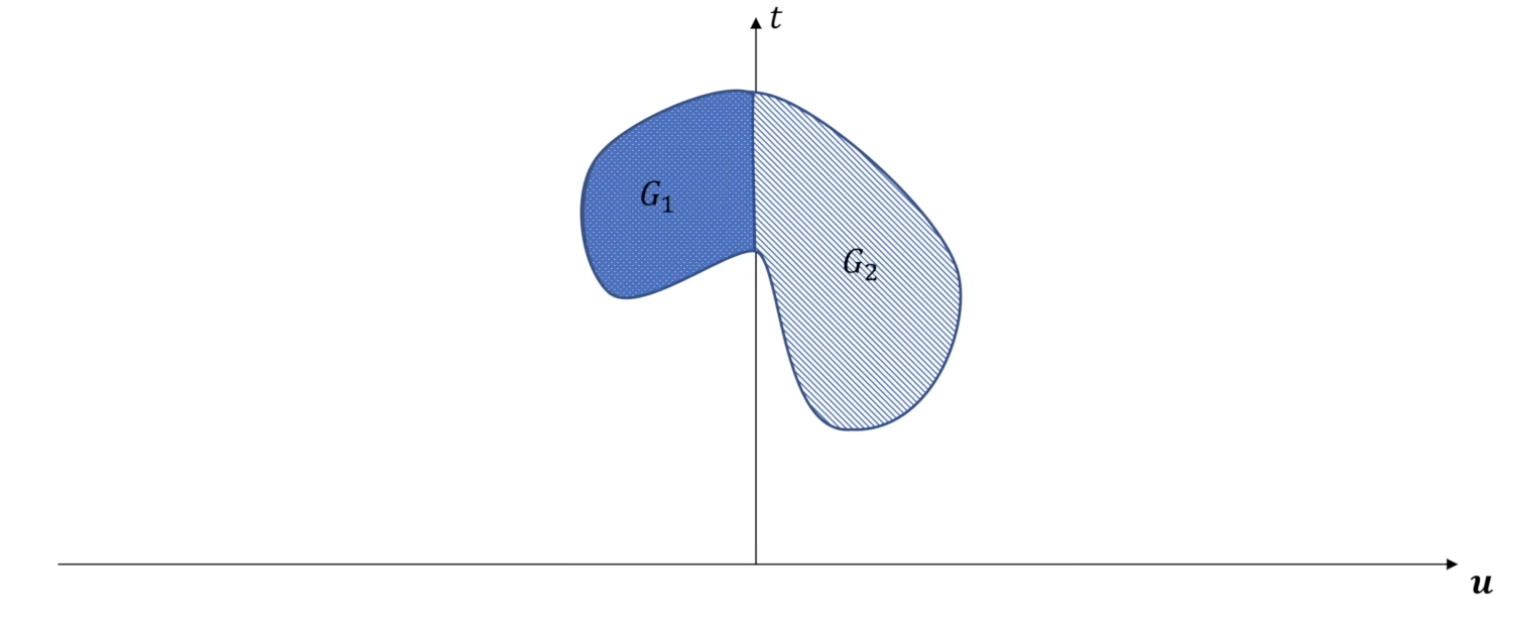
注意，这里G1的部分也有G2
那么对于原问题的解，我们很容易看出就是G1中最下面的那个点，即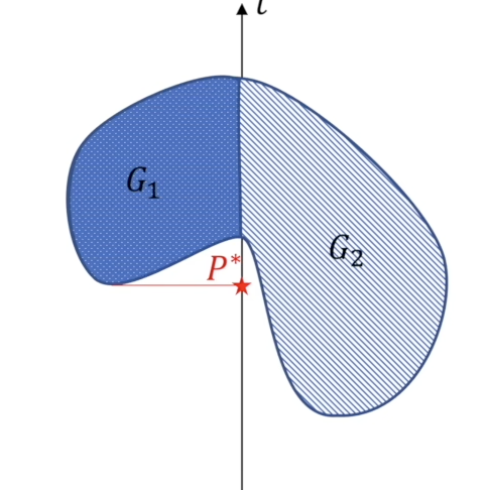
对于对偶问题的解，我们可以看作是先保证斜率不变的情况下，求最短的截距。

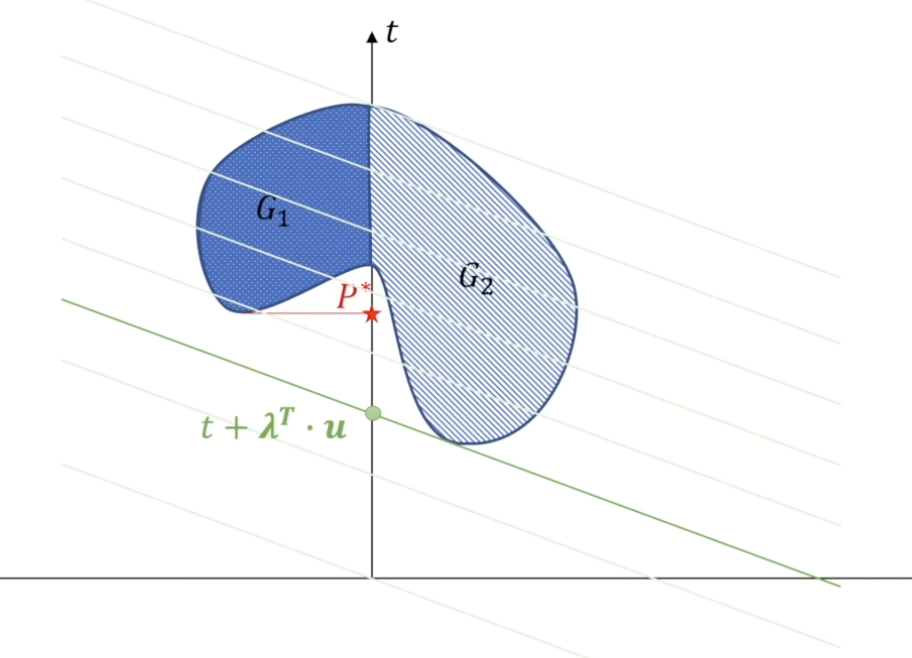
然后再保证经过某个特定的(t,u)点的情况下，对斜率进行变换，然后求出最大的那个截距。

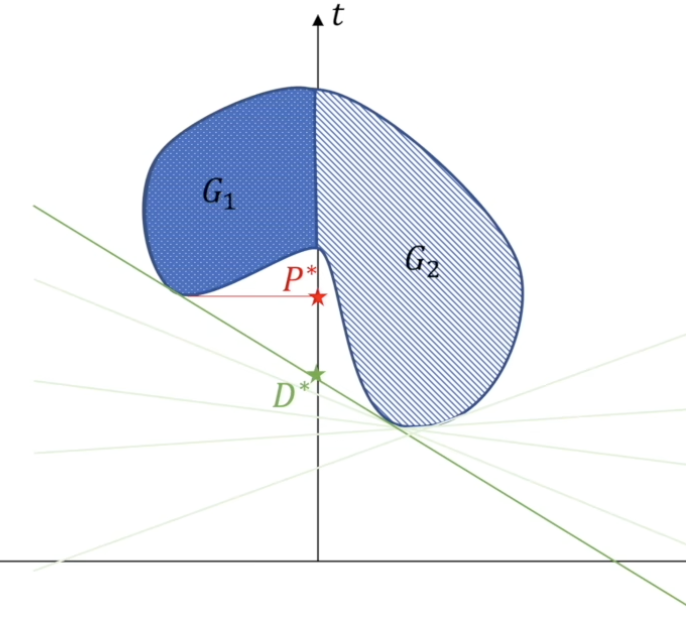
注意，这里由于G1也属于G2，因此，如果直线穿过G1，那么直线也穿过G2，那么就不满足第一个min的条件了，还可以再在斜率不变的情况下降低一些截距。
因此，想要同时达成两个条件，当且仅当直线和G2的解的最小值相切，又和左边G1的最小值相切的情况。即下图所示

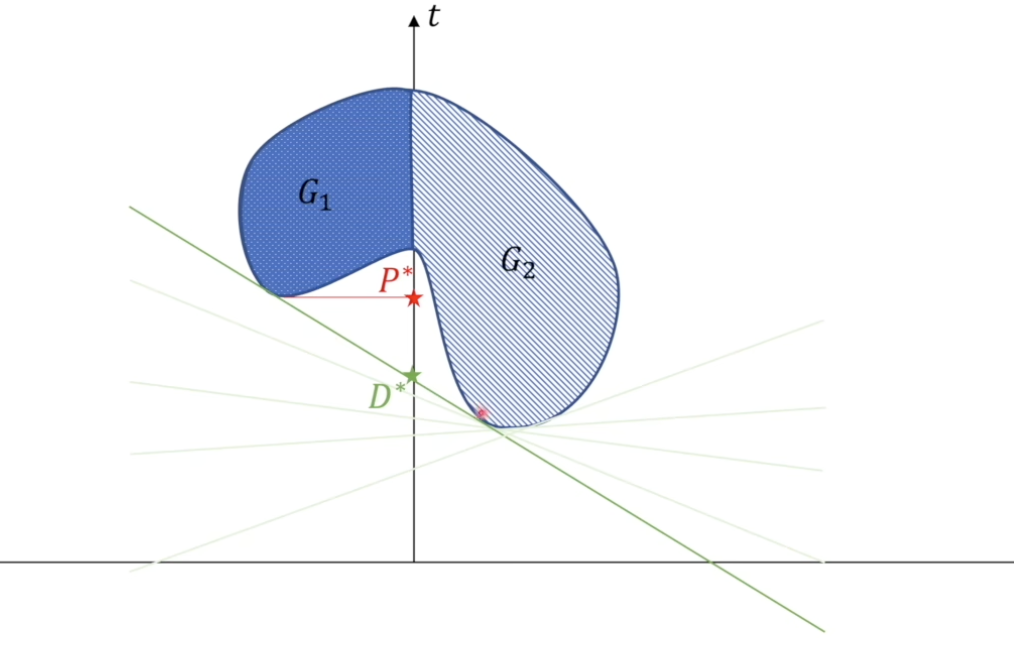
显然，我们可以看出，

我们称的情况为弱对偶，而情况为强对偶。

那么什么情况会产生强对偶呢？不难想象，当我们的可行域是一个凸集的情况下，一定是强对偶。即：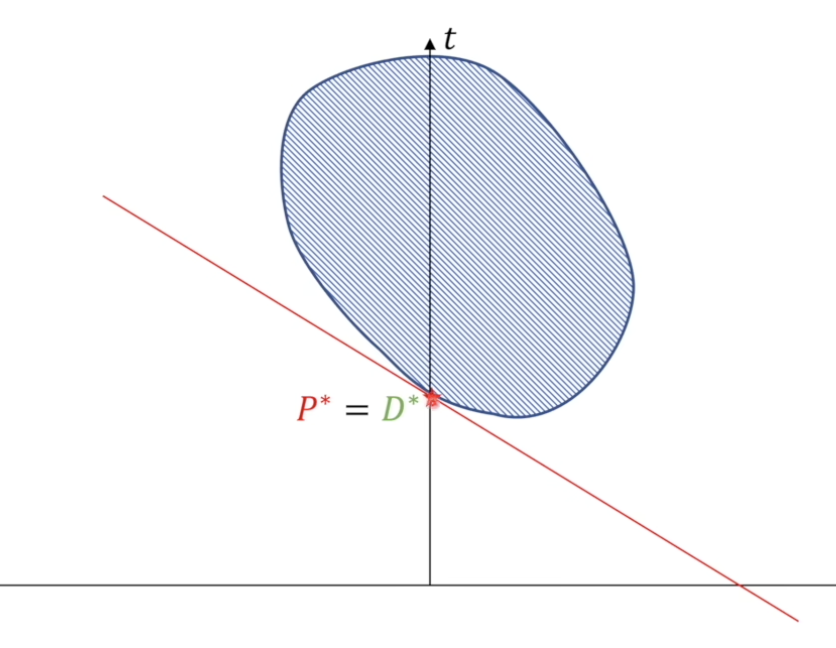

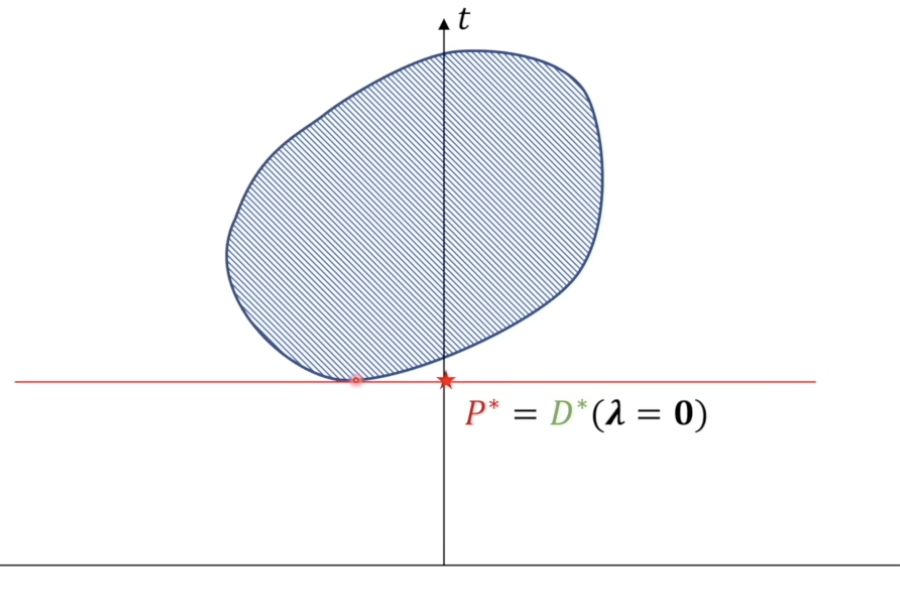
无论是这两种情况哪一种，只要满足可行域是凸集，那么就一定有强对偶关系。

到这里位置，工程上的应用基本就够了，但是如果从数学上来讲，更严谨的强对偶关系在可行域是凸集的前提下，还要满足一个slater条件：
即，可行域内部存在一个点x，x属于仿射集，使得
slater条件是一个强对偶关系的充分条件。

不过证明可行域是凸集还是有难度，一般我们可以用KKT条件来证明强对偶关系。
即

容易知道，前四个都是我们转化为拉格朗日乘数法的基本条件。而最后一个，就是之前说的，所有的松弛的约束条件，他们前面的一定都是0，所有的紧致的约束条件，他们的一定等于0.

更本质的来说，其实我们刚刚看到的两种强对偶关系的解空间就能够说明互补松弛条件了。

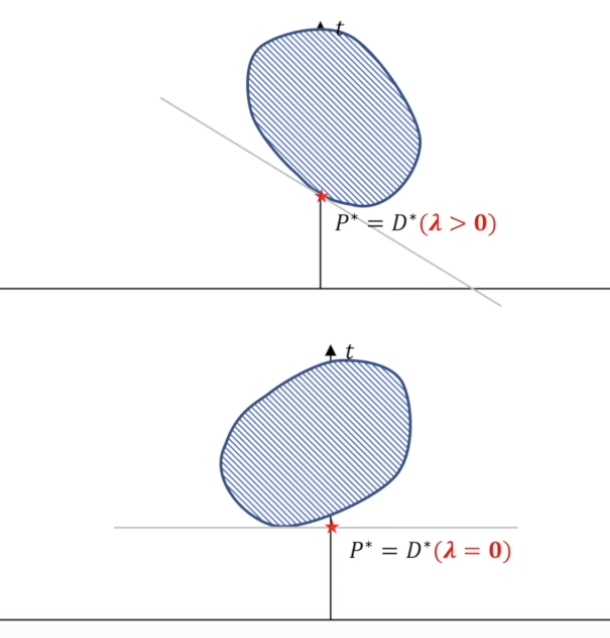
在第一种可能中，对应的是对偶问题的的情况，也就是极值点就在一个约束条件的边界上。对于这种情况，显然我们的解不在全局的最小值上，而是在被限制的可行域内的最小值上。
对于第二种可能，由于所有的限制条件都是松弛的，那么，我们的解就是全局的最小值！