正则表达式和有限状态自动机——泵引理

首先给出正则表达式和正则集的形式定义：
定义字母表T上的一个正则表达式和它表示的正则集，可递归定义如下：
(1)和都是正则表达式，分别对应和
(2)任意是正则表达式，它表示的正则集是{}
(3)如果A和B是正则表达式，分别表示的正则集是L(A)和L(B)，则(A+B)、(AB)、(A*)也都是正则式，分别表示的正则集是
仅由有限次使用以上三步定义的表达式，称为字母表T上的正则式
为便于理解，给出下图

给定文法，求正则表达式

联立方程法：
为了使用这个方法，我们必须先定义一个公理，方便将方程的特定形式转化为正则式
公理：设那么我们有解
公理的直观理解是：x有两个生成式，一个推出ax，一个推出b，那么很显然，一旦推出b，那么就终止了。所以解
基于此，对于任意的G的生成式，我们可以将生成式先转化为类似的方程，然后联立求解得到解。
例1

得到以下方程

将下面的式子带入上面得到

然后我们提出S得到

最后运用公理得到

即得正则表达式
总之，通过以上方法，我们成功创造了一个方法，将生成式转化为正则表达式，也证明了正则文法和正则表达式的等价性。

右线性文法和NFA

本小节我们将试图讨论一种算法，能够直接将右线性文法转化为NFA，减少计算
首先，我们引入引理1
引理1 对于任意一个右线性文法，都可以找到一个与之等价的，产生式形式为的右线性文法。（同样支持的形式)
接下来我们给出算法
对于右线性文法，我们构造NFA，，其中

最重要的，的定义如下
当那么
当那么

（上述算法中的H状态，其实可以理解为结束状态，也就是达到终结符的状态）
下面我们给出一道例题来运用以上算法

正则表达式和DFA

课本上首先给出了一个最重要的定理，对于一个正则表达式R，他所表达的的语言是L，那么一定存在一个-NFA接受语言L
课本对这个定理的证明并没有详细的讲述，但是，它为我们规划了一个思路，对于一个正则表达式，如果我们想要构造一个自动机来识别其所表达的语言，那么我们可以先转化为一个来表达它，然后，利用前面所介绍的算法，转化为NFA，然后再转化为DFA，最后再对DFA消去一些不必要的冗余状态，最后得到最精简的DFA。
下面我们介绍算法来将正则式转化为
首先给出基础的定义，这是显然的

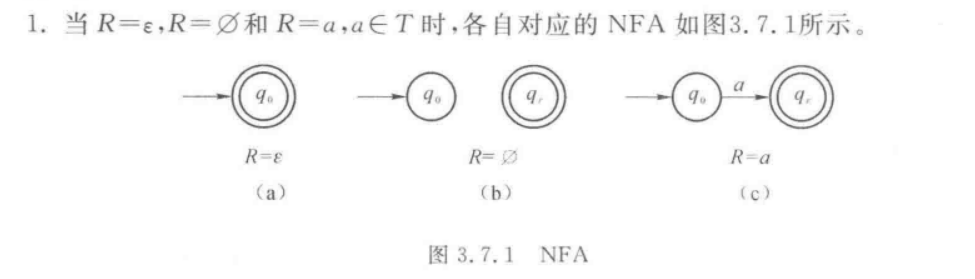
接下来，我们就是运用不同的方法，把以上这些基础定义拼凑起来即可。

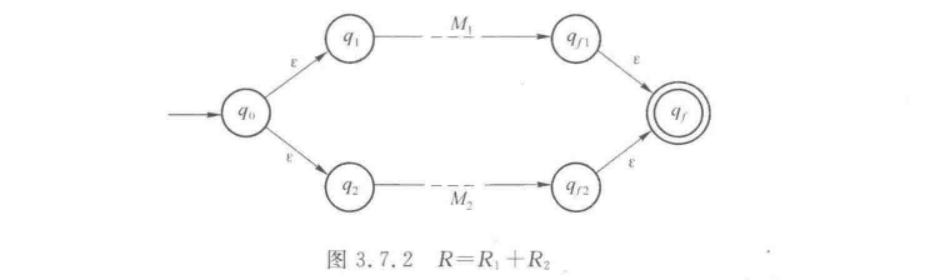
对于R = R1+R2

这个其实类似于一个“并联”的感觉，因为它其实本质就是多了一条可以“同时”走的路罢了
但是由于我们有要求，只能有一个终态，一个初始状态
因此我们只能多添两个头，一个开始头，一个结束头，然后用把他们接入，就可以了
如下图所示

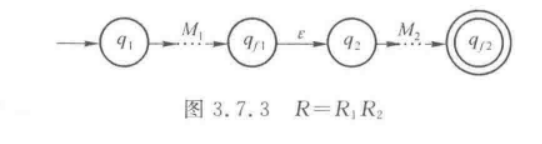
对于R = R1R2

这种类似于一个“串联”的感觉，是要先走完R1，再走R2，就是直接按顺序链接。
对于这种，我们只需要直接用一个键把他们连起来就好了

对于R = R*

这个情况稍微有些特殊，它意味着该状态可以重复下去，即允许我们回到上一个状态，因此我们需要一条反向边来让它回到以前的状态
但是，由于要求中有，说不能有边进入初始态，不能有边从终态出来，因此我们借鉴R = R1+R2的方法，填入首尾状态并通过连入就可以了

特别需要注意的是，由于科林闭包含有空串的情况，因此要在初始态和终态之间加入一条键

下面我们用一个例子，来测试一下以上的算法
例2 对于正则式，构造出不确定的有限自动机
首先，我们分析一下，将他拆为和
然后分别处理，最后连接起来即可
对于ab，我们只要分开处理a和b，然后链接即可。
最后得到

在书中的下一章中提到了右线性文法和有限状态自动机的表达能力是相同的。这其实是不必要的，因为其实，我们已经证明了，右线性文法和正则表达式的等价性，由此，再加上上面证明的正则表达式和有限状态自动机的等价性，就已经可以推出来了。（最上面有通过右线性文法求正则表达式的算法）

那么既然我们已经完成了将正则表达式转化为的过程，那么接下来就是把这个化简的过程了。首先我们省略它化简到DFA的过程，因为已经讲过了。
那么，我们该处理的，就是把DFA化简到最简DFA的过程。

DFA-最简DFA：填表法

首先，为了化简，我们肯定要知道什么样的状态是冗余的。那么，我们给出状态等价（冗余）的定义
定义 设有限自动机 对不同的状态 ，和每个，如果有
q1经过任意的w，都可以到达（任意的）接收状态，q2也同样，那么就说q1和q2是等价的
换言之，如果对于任何一个在输入字符集合闭包中的字符串，q1和q2都可以到达任意一个接收状态，那么我们说他们是等价的。
反之我们说q1，q2是可区分的
如果不存在任何，能够达到状态q，那么我们说状态q是不可达的。
根据定义可知，如果一个DFA，不存在不可达状态和没有冗余状态，那么这个DFA就是最小化的

以下给出填表法，递归地计算出不等价的所有状态
首先，我们给出归纳的基础。对于所有的终结状态和非终结状态，他们是可区分的。因为对于他们不可以都到达接收状态。
其次，给出我们的归纳过程
假设p和q是可区分的，如果状态r和s通过某个输入符号a，可以分别转移到p和q，就意味着r和s是可区分的。
这个也很好理解，对于输入符号，状态r达到了终结状态，但是状态s没有达到终结状态。因此可以推出r和s是可区分的。
基于此，我们可以给出填表算法。
第一步 标记终结态和非终结态之间的状态对为可区分的

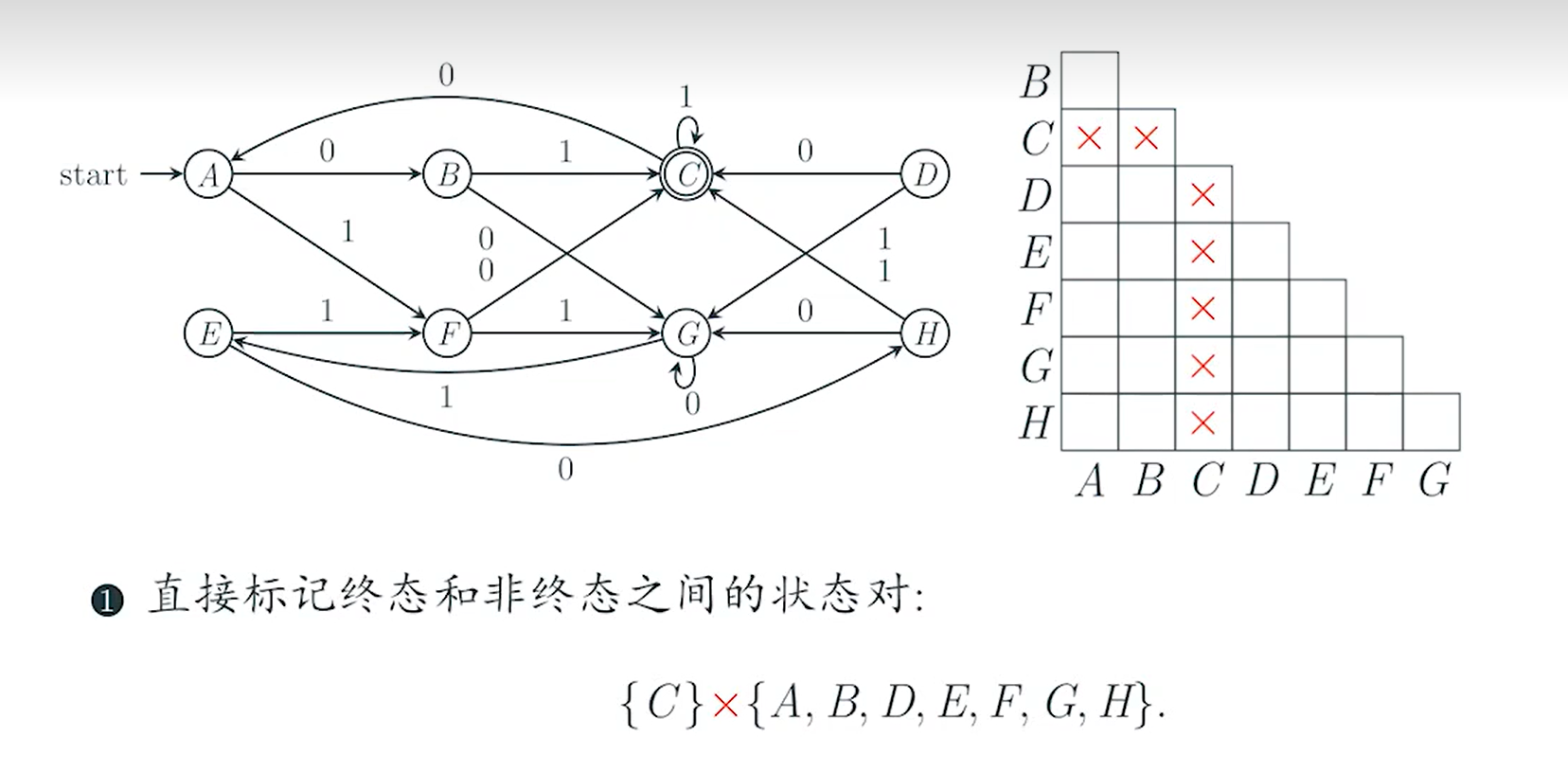
第二步 任取，这里为了简便处理，我们从长度为1的0开始，接下来再试试长度为1的1，然后再试长度为2的，往下循环直到差不多填满为止


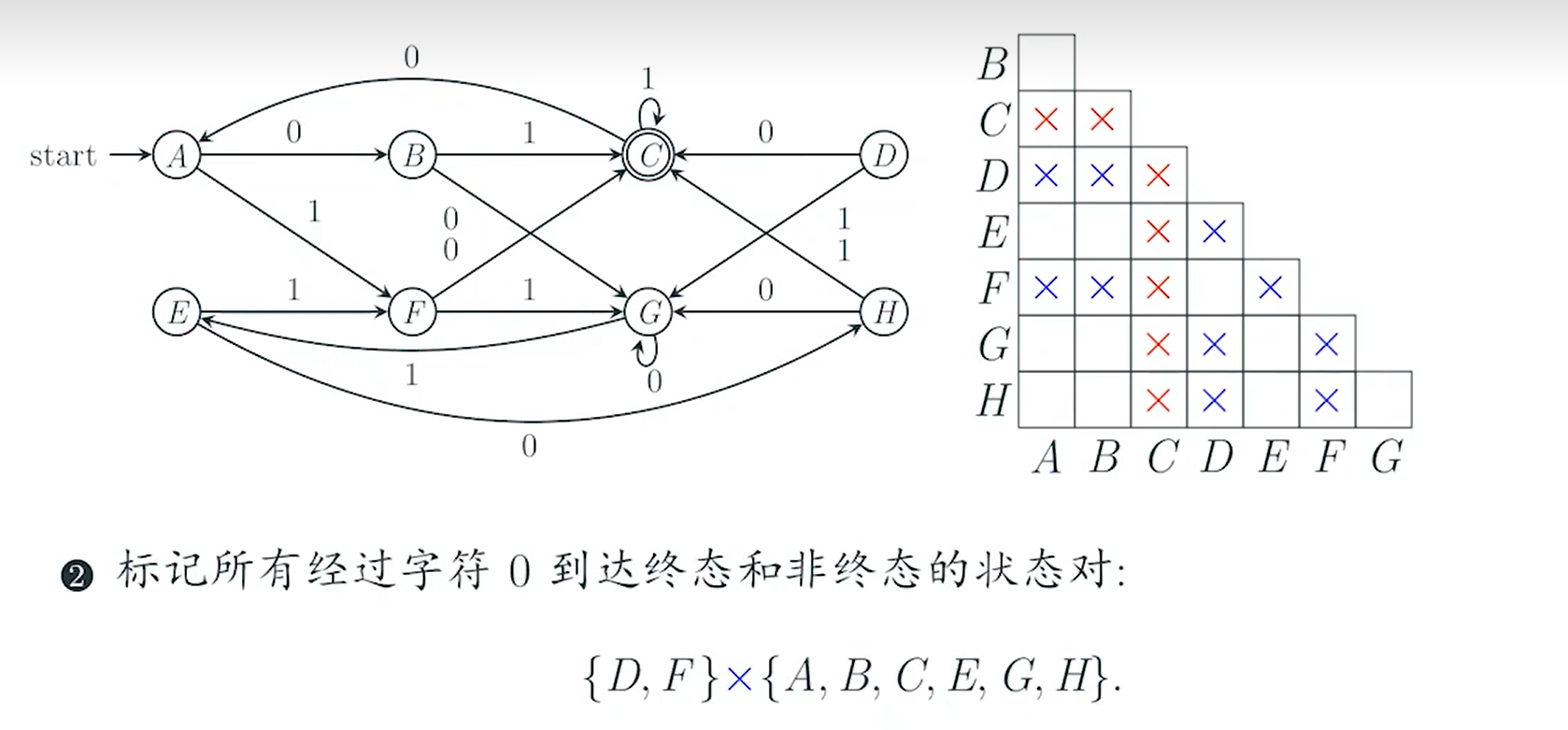
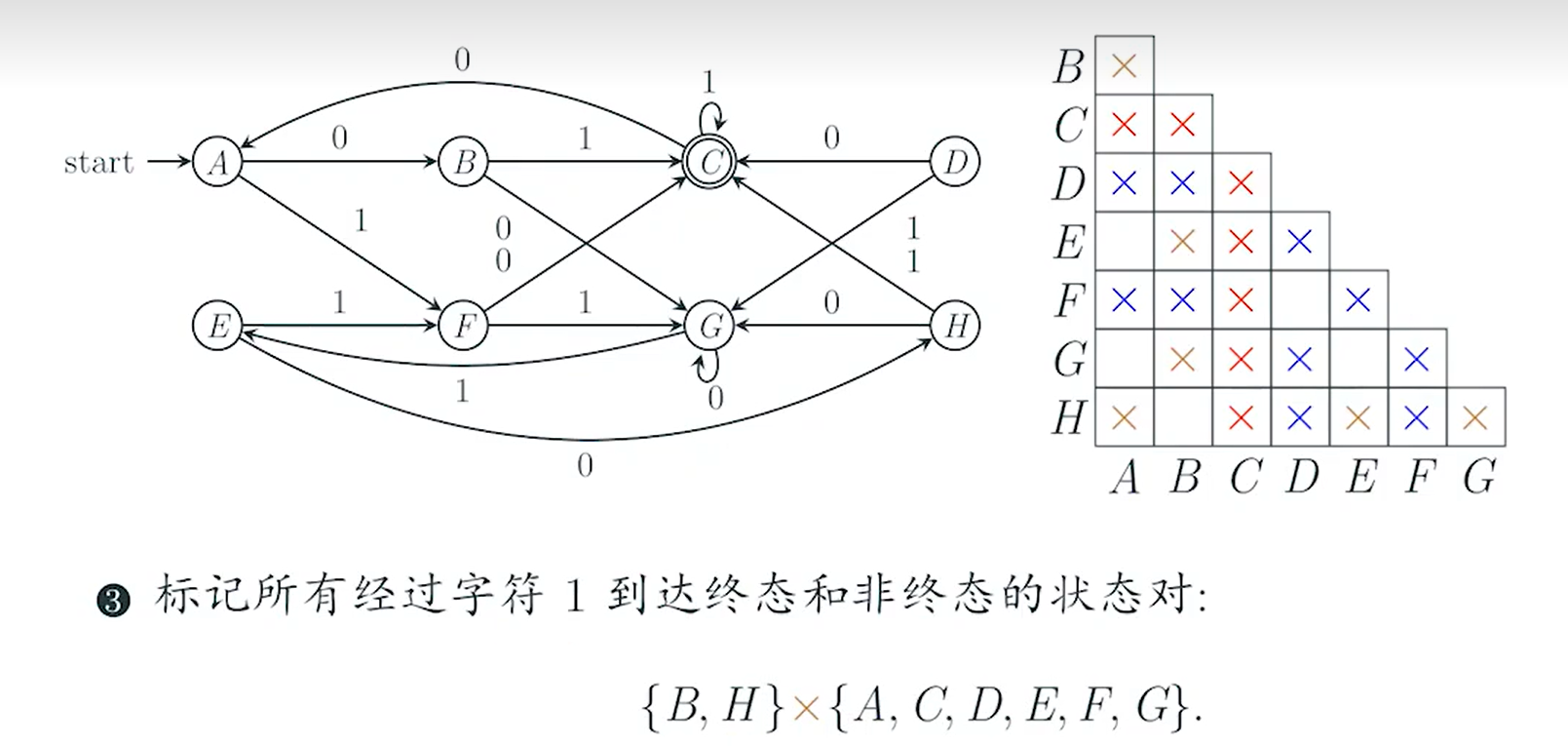
此时剩下的空已经很少了，我们只需要逐个检查这几个空就可以了。


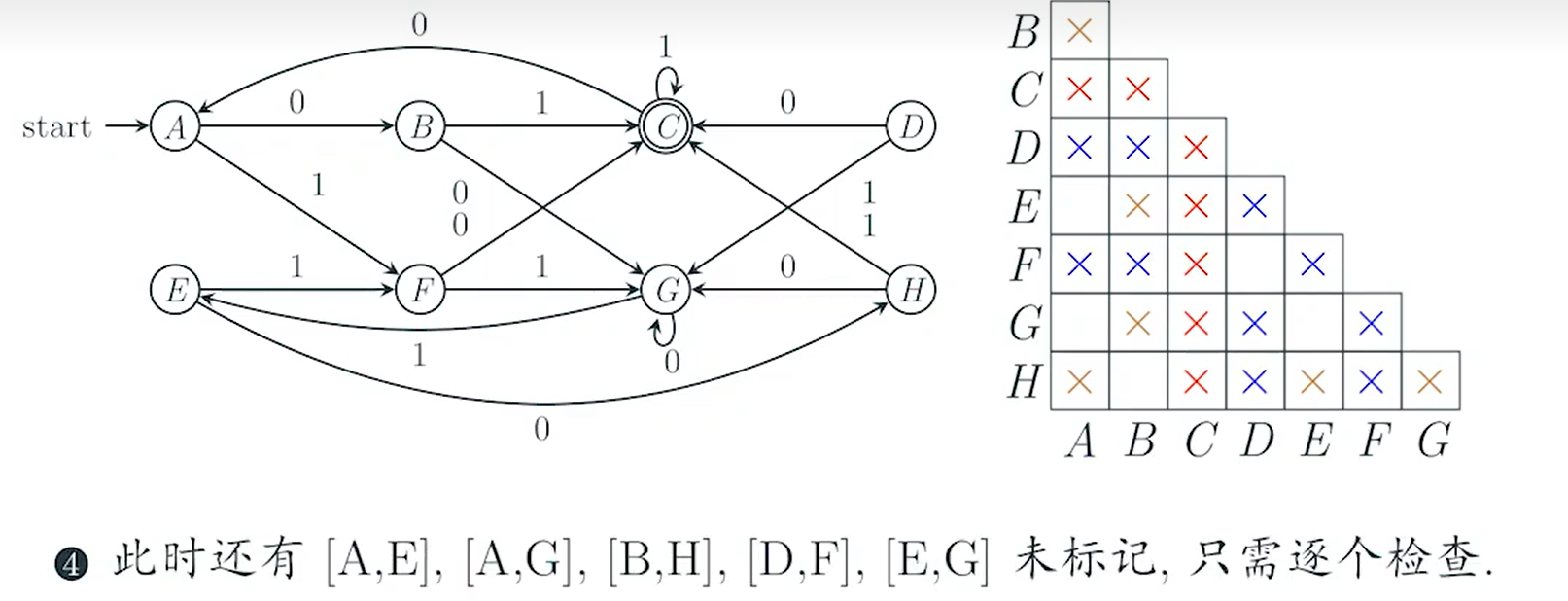
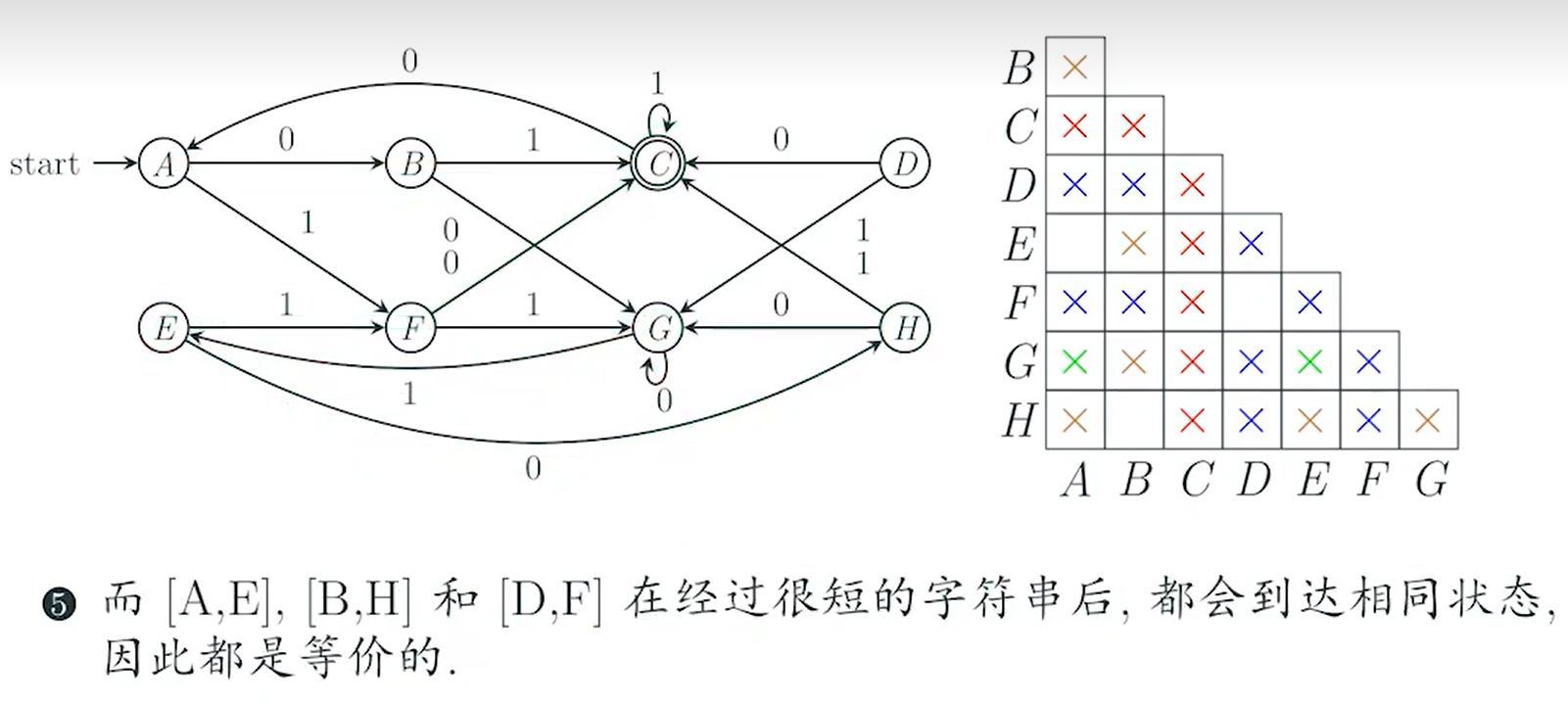
检查的方式为，看看他们能不能通过w到达可区分的状态对就好了。
如果可以通过相同的字符串，到达可区分的状态对，那么可以直接判断他们是可区分的。
但是！注意，如果要证明他们是不可区分的，一定要遍历所有的w的情况，也就是判断所有的输入的可能性！！（因为定义是任意的）
也就是说其实这个证明方法，只能用来手算，没法程序化 TAT

泵引理

泵引理的作用：用于证明一个语言是不是正则集
首先给出其直观的理解。
这里书上的证明其实少了一些东西。我们的正则集，其实包含两种，一种是有限集，一种是无限集。对于所有的有限集，我们很容易证明他们都是正则集，因此这里省略掉了。所以，泵引理的讨论范围，都是在形如的无限集的情况下讨论的。
对于泵引理的证明，可以简单理解为鸽巢原理的运用。
我们采用反证法（个人认为书上这里的证明写的不对，因为不一定每个语言都可以被有限状态自动机表示，所以要用反证法）
我们假设这个语言是一个正则集，那么它就可以被一个DFA表示，我们假设这个DFA有n个状态，那么我们取一个字符串 ，那么一定就有至少经过了n+1个状态，那么在这个情况下，一定有某一个状态是多余的，我们也就是这个识别过程有一个环。
那么这个环是可以重复很多次的，也就是泵引理中可以重复的那部分。
因此我们给出最终的形式定义
如果语言L是正则的，那么，只要，就可以将w分为三部分，，满足：
1、
2、
3、 （注意等于0的地方，可以往少了泵）
注意，这个w的分法，是不唯一，但是有界的。y最短也得是DFA中那个“环”的长度，不可以短于这个长度

泵引理的应用：证明语言是否是正则集
这里有很多巧劲，下面给出一个例子


这道例题就是往少了泵的典型
这一部分的关键是w的取法，一定要让利用的这个式子，让y处于一个比较“暧昧”的位置，限制其形式。
所以，基本上泵引理只能证明一个语言不是正则集，不能证明它是正则集，因为没法取遍所有的w…

还有这种，需要分类讨论的
总之基本就是把上面的小n换成大N，然后想办法证明就对了

但是，有的时候，直接使用泵引理来证明，对于一些比较复杂的情况是很难的。
我们可以利用正则语言对==并交补差连接闭包运算的封闭性==，来简化一部分证明。
即把大问题化归到小问题上来解决。

正难则反问题

这种就比较难想了，只要求了解吧

带输出的状态机——摩尔机和米兰机

这一块基本和上学期的数电部分差不多，核心难点在于设计。
主要的设计范式，是需要吧状态赋予意义。这点是最难的。
往往在设计米兰机/摩尔机的时候，我们需要对状态赋予一个现实意义。
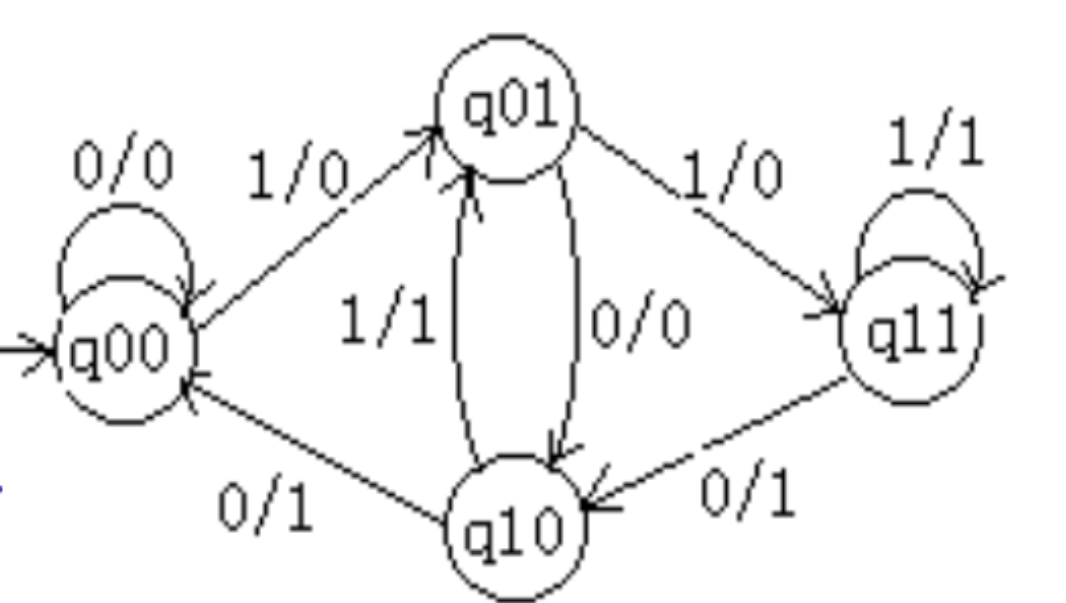
例3 设计米兰机，输入是0,1组成的串，要求输出对输入延迟两个时间单位
那么我们就要“记住”前两个的输入是什么
得到如下的结果