GENERALIST REWARD MODELS- FOUND INSIDE LARGE LANGUAGE MODELS
前置准备:Maximum Entropy IRL
要理解周老师的这篇最新的作品,势必要先理解这篇Maximum Entropy IRL。IRL的工作主要是在给定专家行为轨迹的情况下,模仿学习出一个新的模型,因此被称作逆强化学习。
我们知道,逆强化学习的过程的核心问题在于模糊化。即,对于给定的轨迹,可能有多个奖励分布符合条件。但是,本篇的工作主要采用最大熵原理,即使用最大熵的奖励模型来拟合。
由于最大熵模型的解的形式必然是指数族分布,那么我们势必就可以用指数族分布来参数化轨迹的概率网络。本篇采用玻尔兹曼分布进行参数化。
其中,
至于为什么采用玻尔兹曼分布,这里做一个简要的说明。由于本篇的工作可以概括为:
1. 概率之和为1:
2. 特征期望匹配:
的条件下,最大化
运用拉格朗日乘数法进行求导求解之后,得到的形式便是玻尔兹曼分布。
接下来,这篇工作运用极大似然估计的原理,构建似然
对其求导我们可以得到
这个公式的含义是:“上山”的方向 =
(专家的平均行为特征) - (当前模型 πθ
的平均行为特征)
: 是我们从数据中直接观察到的、专家所有演示路径的平均特征。这是一个已知的、固定的值。 : 是在我们当前的奖励权重 θ下,模型自己预测的所有可能路径的加权平均特征。这是一个需要计算的值。
因此,通过梯度上升的算法,我们便可以求解出最大似然下的参数
本篇要解决的问题
目前,LLM在对齐领域不可避免的需要依赖外部的奖励模型。我们不得不花费大量的成本来标注一个具有人类偏好的数据集。并用它来训练一个独立的奖励模型。
为了避免人工成本,研究者们提出用RLAIF的方法来对齐更强的AI。但是这些方法通常是启发式的,缺乏理论基础,容易让学生模型学到裁判模型的风格偏见。
相关工作包括:RLHF,RLAIF,IRL,DPO等
本篇核心观点
这篇论文的核心贡献是提出了一个颠覆性的发现:一个强大的、通用的奖励模型,根本不需要从外部构建,因为它已经内在地、潜在地存在于任何通过标准“下一个词元预测”训练的语言模型之中。作者将这种奖励称为 “内生奖励”(Endogenous Reward)。
作者首先指出,RLHF范式本质上是一个简化过的IRL过程。
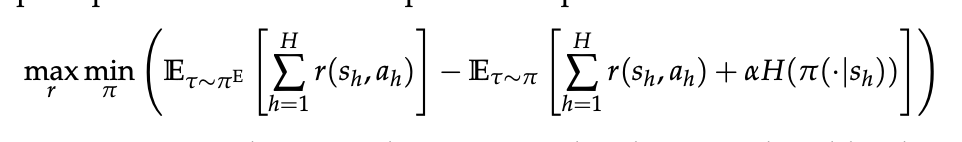
这是原最大熵IRL论文中目标函数的对偶形式。这里不做详细的理论推导。但是由于在最大熵的框架下,一个理性智能体的行为概率分布,应该与其获得的回报呈指数关系。我们可以假设
因此,我们容易看出,这个博弈函数的纳什均衡在于,无论如何改变
因此我们对函数进行求导可以看出,
当且仅当二者期望相同的时候,我们能够取得极值点。因此和我们原来的最大熵的原理的假设一致。
这个公式的目标,可以看作是RLHF中使用的那个reward
model的一个更通用的、分布层面的公式化的描述。他不再通过学习赢家和输家之间的得分差异来学习一个奖励函数,而是比较整个专家分布在奖励模型下产生的最优竞争策略
其中的min项会找到最强的模型,max项会找到能够区分二人的奖励函数,让基础模型可以更好的学习专家模型。
从这个角度看,RLHF的奖励建模过程可以被解释为IRL原理的一个实践上、计算上易于处理的实例化 。RLHF并没有去解决那个复杂的‘min’优化问题,而是将其简化,直接在偏好数据集中最大化“赢家”和“输家”之间的奖励差额 。因此,BT模型是IRL提供的更广泛理论框架中的一个特例 。我们的工作回归到这个更通用的IRL公式,以便直接推导出一个奖励函数,而无需进行显式的成对比较。
于是,作者提出我们可以直接用一个更基础的IRL方法来恢复那个能够最好的解释专家数据集上的奖励函数。但是由于大部分的IRL方法都是适用于在线学习的。因此作者引入了inverse
soft
Q-learning的离线IRL方法来构建这个问题。该方法旨在找到一个能够最好地解释静态数据集D中专家数据的Q函数。即解决下面这个优化问题:
一旦我们成功找出了最优的Q函数,那么,理想的奖励函数便可以通过逆向软贝尔曼算子来恢复,即:
作者这里的核心观点就是:
这刚好就是next token
prediction的目标函数。因此作者总结了如下的命题:

于是,我们可以将LLM得到的logits,直接作为Q函数代入到方程中,最终解得奖励的形式:
由此,作者还提出,GenRM也是这个框架下的一个特殊情况。即
后续作者提供了这个方法的一些理论辩护,主要给出的启示是:
- 基础模型的模仿能力,直接决定了从它内部提取出的奖励模型的判断能力
-
RL训练方法得到的误差并不会积累,而模仿学习的误差会积累,并且是平方的速率积累
-
这种自我进化式的方法,实际上并不能持续提升自我,从自我提取出的内生奖励,恰好就是之前的最优奖励,这个过程会逐步收敛于一个最优的策略,从而停止进化。
实验
RMBench跑分
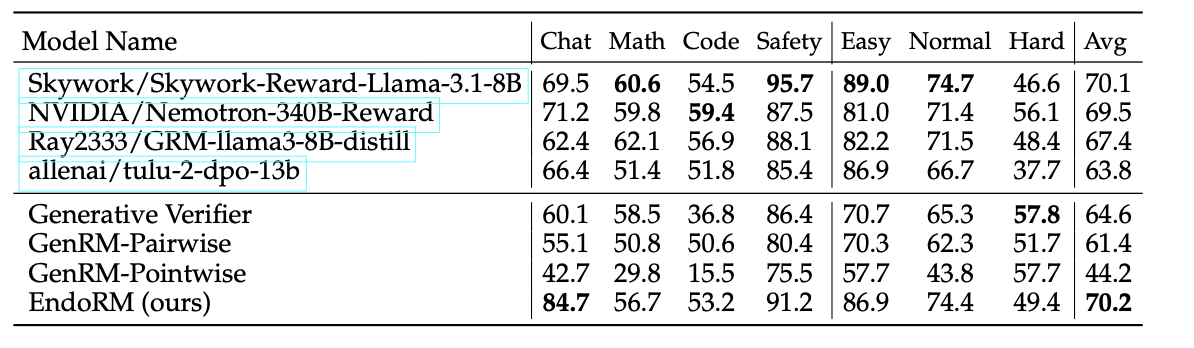
前四个都是有深度训练过的RM model,而下面这四个都是无需训练的RM
model。
可以看到,作者的方法爆了所有的无需训练的方法,同时在平均能力上达到了最优。
遵循指令的能力
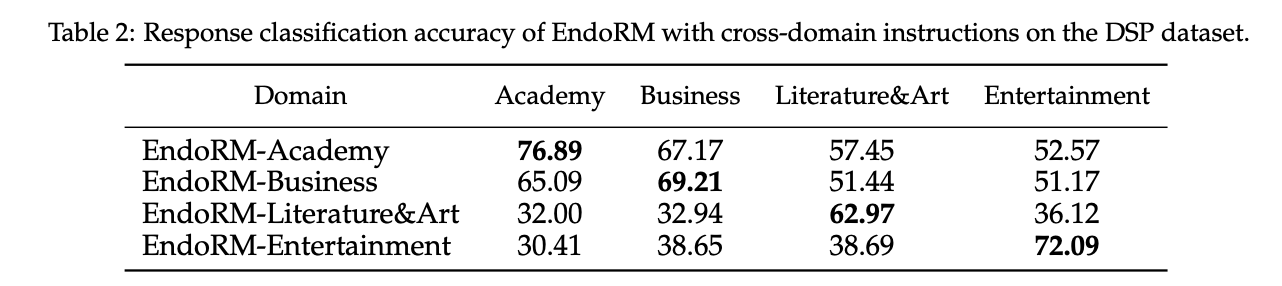
即能够根据提供的prompt,在领域内问题进行相应的回答,确实表现出了指令遵循的能力。不过没有理解为什么做这个实验。
自我提升的能力

通过这个图,他对自己进行了RL的微调,确实增强了模型的能力。
如果您喜欢我的文章,可以考虑打赏以支持我继续创作.




