7.5阅读笔记

Scaling Test-Time Compute Without Verification or RL is Suboptimal

要解决的问题

本篇工作是讨论性质的，旨在讨论Verifier是否是必须的一个组成部分。Verifier主要是对答案进行一个明确的验证信号 ，来引导RL或者是启发式算法。而无Verifier的方法主要是通过SFT对专家轨迹进行克隆。
阅读之前个人的一些insight：
我认为，其实重点并不是Verifier，而是RL。RL的探索能力能够允许模型的能力超出专家的水平，这个是最重要的，也即模型的探索-利用能力。从这个角度考虑，RL的目的不是简单的对齐人类，而是对齐奖励。即在一定的规则下的能力。

相关工作

VB方法：主要是探索不同的验证信号，包括Rule-based方法或者是专门的RM来信号的产生
VF方法：主要是从强大的模型中蒸馏。通过对大模型的长链思考过程的转化，让小模型进行模仿。

核心论点

作者提出，基于验证器（VB）的方法远优于无验证器（VF）的方法，并且随着计算预算的增加，这种优势会越来越大 。
作者解释，这个原因是因为LLM中存在两个关键特性，即异质性和反集中性。
- 异质性 (Heterogeneity)：指基础LLM在解决同一个问题时，有能力生成多种多样的、不同风格、不同长度的正确解法 。

• 反集中性 (Anti-concentration)：指基础LLM在自己生成的众多解法中，有不可忽略的概率（a non-trivial probability）会碰巧生成一些比它自己的平均水平要好的解法 。

基于这两个特性，论文做了如下的论证。
- 异质性对VF方法有害：对于一个充满多样性的基础模型，VF方法（如SFT）试图去“模仿”所有这些五花八门的正确解法，这是一个非常困难的学习任务，导致其性能不佳 。

• 异质性对VB方法有益：只要模型同时满足“反集中性”，这种多样性反而为VB方法（如RL）提供了丰富的探索空间。RL可以利用奖励信号，发现并放大那些“比平均水平更好”的解法，从而实现有效的学习 。

主要理论结果：当基础LLM同时满足这两个在实践中很常见的条件时，随着测试时计算预算（H）的增加，VB和VF方法之间的性能差距会以Ω(√H)的速度被拉大 。这意味着，验证（Verification）是实现未来计算扩展的关键。

次要insight和理论推理的方法论

• 本文对比两个算法哪个更好，就是通过对比他们得到的总奖励来判断。即
  
• VF方法的性能极度依赖专家算法的选择，我们需要保证：1、专家能够进行有效的推理，即得到的总奖励很高；2、在保证1的前提下，专家要尽量的贴近基础模型的分布。不然就容易产生”博士教小学生“的无法对话的错误。博士解释1+1可能用群论，小学生完全听不懂。
  具体而言，作者在以下的这个球中寻找得到总奖励最高的专家，参数是分布近似的”距离“，也就是球的半径。
  
• 作者在本篇中实现了对异质性的定量分析。具体而言，是通过对同一问题时，生成解法轨迹的多样性程度来衡量，即方差。具体而言，是通过下面这个式子来的
  个人认为，作者在这里为了后续推导的便利进行了简化的操作。主要是用动作价值函数的方差来衡量异质性是不够完善的。因为根据异质性的定义，完全可能存在不同解法但是得到的奖励近似的推导过程，因此这里是不够完善的。可以用cos相似度对推导步骤进行similarity的判断应该会更合理一些。
  
• 专家异质性的下界是：
  其中，是基础模型，也就是我们要进行训练的那个模型。是专家模型。分别对应两者的异质性的量。
  
• Verifier的准确性上界：其中

  • ：是预测值和真实值之间的绝对误差。

  • ：是我们的验证器预测的奖励。可以理解为“模型的打分”。

  • ：是对于一条推理轨迹 τ 的真实奖励（ground-truth reward）。可以理解为“标准答案”。

  • ：代表对所有可能的问题（来自问题分布 ρ）和所有可能由基础模型 πb​ 生成的推理轨迹，求取这个误差的数学期望（平均值）。

  • ：代表训练样本的数量。这是最重要的变量，它在分母上，意味着训练数据越多，n 越大，误差上界就越小。这是符合直觉的：学的越多，懂得越多，犯错就越少。

  • ：代表推理轨迹的最大长度（horizon）。H 越大，意味着推理过程越长，问题可能越复杂，学习的难度也越大，所以误差上界会相应变大。

  • : 代表所有可能的奖励函数（即验证器）组成的函数类的规模。这个值越大，意味着“正确答案”可能的形式越多、越复杂，学习的难度也就越大，误差上界也会变大。

  • ：代表这个不等式成立的不确定度，可以理解为是检验里面的”不把握程度“。我们希望这个值尽可能的小。很明显，对于Verifier学习能力的上界的宽松程度会影响该值的确定。

  • ：是一种“大O符号”，表示右侧的界限忽略了一些与 H 相关的对数等多项式因子，主要关注核心的增长趋势。
    

• VF算法和真实最优模型之间存在信息论上的下界。
  它代表了，在最优专家策略，最好的奖励模型的情况下，用vf的方法至少会有这样的一个奖励上的偏差，这个无法通过算法来优化。并且，这个差距和你学习的专家的异质性有着直接的正比关系。
  其中
  • 是在专家集中最优的那个专家模型
    
  • 是你通过vf方法，在n个数据中训练出的模型
    
  • 是专家异质性的中位数。
    
• 作者接下来定量分析反集中性：
  这个公式衡量了在具体问题x上，模型表现出”惊喜“的概率。
  其中：

  • :代表基础模型在解决问题x时的平均得分
    

  • :代表模型在解决问题x时得分的标准差，衡量了得分的波动范围
    

  • :代表一个惊喜的门槛，他是一个基于标准差的浮动值。
    

  • :代表概率
    所以， 的整体含义是：基础模型 πb​ 在解决问题 x 时，其单次表现的得分超过“平均分 + 一个惊喜门槛”的概率。简单来说，就是模型在该问题上“超常发挥”的概率。
    最后，作者通过这个式子，完成了反集中性的定量：
    
    其中，指在中最好的模型。即最优专家策略。
    

  • ：这个值代表了在问题 x 上，最优专家策略 相对于基础模型​ 的“改进空间”有多大。可以理解为解决这个问题所需要的“学习难度”。

  • ：将这个“改进空间” 代入上面的概率公式。它衡量的是，模型有多大的概率能自主生成一个足够好的解法，这个解法的好坏程度与它需要学习的难度相关。

  • ：这是最关键的一步。 的意思是“取所有问题中最坏的情况”。整个表达式的意思是：即使是在那个最让模型头疼、最不可能产生“惊喜”的问题上，它“超常发挥”的概率也至少要大于一个固定的常数 c（c>0）。
    

• 接下来，为了对比VF算法，作者讨论了一种很简单的VB算法的性能损失的上界。具体公式为：
  通过这个公式，作者衡量了vb算法和最优模型之间的差距，显然，其和无关，而是和反集中性成反比，这说明反集中性越强，模型就能够更好的学习到最优模型的解法。由此，我们可以得出其相比于VF算法的优势。
  
• 最后的最后，作者直接将VF算法和VB算法放在一起比对，得到显然，VB算法要优于VF算法。

这个文章后续的的理论推导和证明相当复杂，涉及到信息论，高阶概率论和高等统计推断的内容。尤其是浓度不等式的应用。简单的看了一眼，感觉作为本科生完全看不懂，对我来说是过于复杂了…感觉被刺激到了括弧笑。兴许笔者过两天会单开一个信息论的笔记栏目，可以期待一下。

实验

实验一 Didactic Setup

实验通过引入这样的一个任务：上下文相关的植入子序列任务。
任务目的：
给定输入，即一串随机的数字，如(1,2,5,3,8)。
我们预先定义一个函数，这个函数是模型不知道的，比如
因此，对于一串输入的随机数字，就会有一串对应的答案，文章把答案成为gold，他的表出：()
我们只需要让模型生成一串数字，只要数字中包含完整的金子序列就算成功。
可以理解为是让模型猜数字找规律的一个游戏。

任务有了，接下来他用一个基于算法规则的程序，记作，其中参数就是理解这个程序的关键，他是调节“专注度”的一个参数，通过调整，我们可以生成不同异质度的数据。越高，它越倾向于直接推出金子序列。反之则会尝试更多的推理，在多次闲逛之后才可能有金子序列。

我们将以上的、具有许多不同的产生的数据杂糅起来，这样我们就得到了一个异质度比较高的数据集。改变输入数据的的分布，我们就可以得到异质度从低到高的数据集。

然后，研究人员利用不同的异质度的数据集对进行微调，得到接受了不同异质度的基础模型
现在，有了统一的“学生”（基础模型 ​），研究人员开始用两种不同的方法来训练它，看谁学得更好。

• VF (无验证器) 方法的实现:

  1. 制作“教材”: 让基础模型 πb​ 去解决一系列问题，然后通过“拒绝采样”（即不断尝试直到成功为止）来收集所有成功的推理轨迹。这些轨迹构成了“专家数据集”。

  2. 进行教学: 使用监督式微调 (SFT) 来训练一个新模型。目标就是让这个新模型尽可能地去模仿这份“专家教材”里的所有成功案例。

• VB (基于验证器) 方法的实现:

  1. 训练“裁判”: 不给模型看标准答案。而是先让基础模型自己去生成各种各样的轨迹（包含成功和失败的），然后给这些轨迹打上真实的奖励分数（0或1）。用这些带标签的数据训练出另一个GPT2-xl模型，让它学会当一个 “验证器”，即预测任意轨迹的奖励。

  2. 进行教学: 使用强化学习 (RL) 来训练一个新模型。这个模型在训练中，不再依赖真实奖励，而是依赖上面训练好的那个“验证器”给出的分数作为奖励信号。】

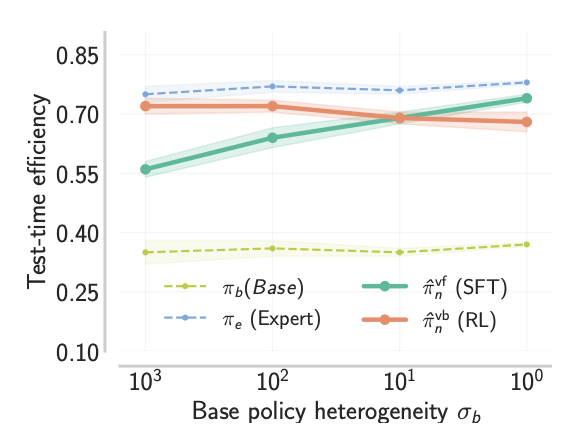
实验结果如上图所示，随着训练数据中的异质度的上升，VB方法逐渐变得有更高的效率，能够更快的给出答案。这体现出了RL在异质性数据上的利用效率。

实验二：大规模数学推理

1. 实验目的

将在教条式环境中关于VF和VB方法扩展性的理论发现，应用于大规模、真实的数学推理基准（MATH benchmark）上，以检验理论的现实意义。

2. 实验设置

• 基础模型: 使用了 Llama-3.1 和 Llama-3.2 的3B和8B模型作为“学生”模型 。

• 任务: 在经典的 MATH数学推理基准 上进行训练和测试 。

3. VF方法的具体实现 (SFT on Stitched Search Traces)

为了让VF方法也能够利用更多的“思考”时间，研究人员采用了一种名为 “在缝合的搜索轨迹上进行SFT” 的方法。

• 如何制作训练数据:

  1. 首先，从基础模型中为同一个问题收集若干个错误的解题尝试。

  2. 再收集一个正确的解题尝试。

  3. 然后，像穿糖葫芦一样，将这些尝试“缝合”在一起，形成一条长长的轨迹，格式为：(问题) -> (错误的回答1) -> (错误的回答2) -> ... -> (正确的回答)。

• 如何训练:

  • 使用监督式微调（SFT）来训练基础模型，让它学习这种“先犯错、后修正”的完整轨迹。

• 目的: 这种方法的意图是教会模型进行迭代式的自我修正，这是一种利用更长计算预算的方式。

4. VB方法的具体实现 (BoN with a Verifier)

这里就用到了BoN方法。

• 如何训练“验证器”:

  1. 从基础模型 ​ 中为每个训练问题生成一定数量的轨迹。

  2. 根据最终答案是否正确，为这些轨迹打上 0（错误）或1（正确） 的标签。

  3. 用这些带标签的数据，以标准的二元交叉熵损失，训练一个与基础模型同样大小的验证器模型 。

• 如何在测试时使用:

  • 在测试时，完全不使用SFT训练出的模型。而是直接用原始的基础模型 ​生成N个候选答案，然后用训练好的验证器从中挑选出最优的那个 。

5. 实验结果及其分析

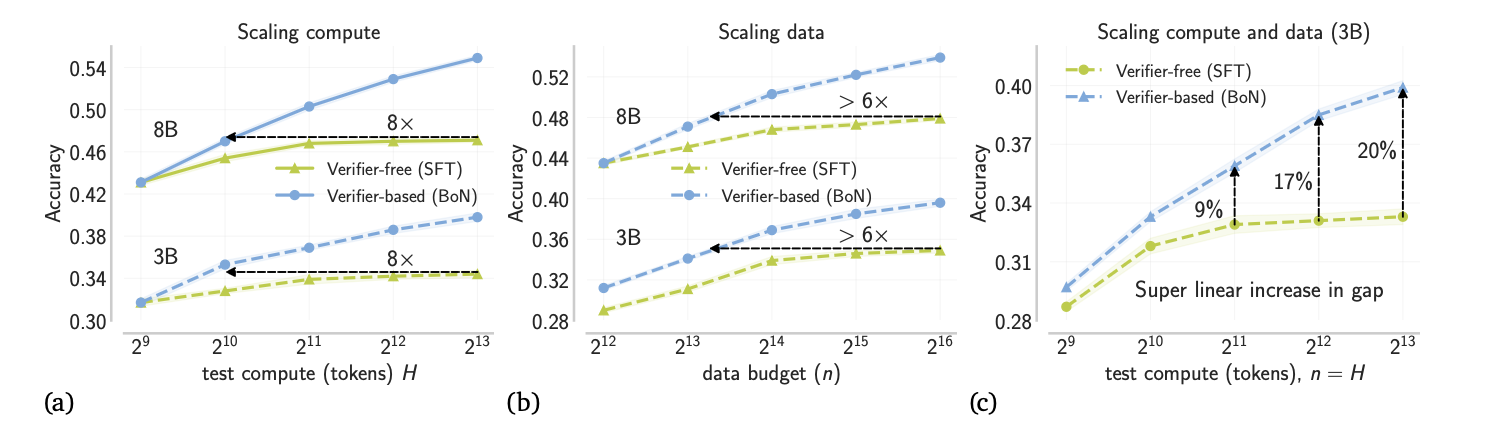
- 在长token环境下，基本上VB方法在计算量上会碾压SFT方法，我认为这是实验造成的问题。主要是实验在设置的时候，VF方法的具体实现用了长轨迹的方法，这使得模型更偏好生成长轨迹，有点问题这里，根据我个人的insight，Parallel的方法肯定是要比long context的方法要耗计算量的（同acc的情况下）。但是无伤大雅，因为计算量本来也不是主要讨论的部分。
- 在训练数据量相同的情况下，VB的方法显示出了更好的准确率，这和我的insight相符。不过这里的x轴选取的都比较大，个人感觉，如果是小一点的话，很可能SFT的方法会更有效一些。这里作者玩了一点小心机吧应该是
- 图c是数据和计算量同时拓展的情况，可以看出，二者的差距在明显的加大。甚至是线性的增加，这很夸张。这是我觉得这个实验最震撼我的一个地方。

总结

本文通过理论分析证明了VB方法远远优于VF方法，并且通过两个典型的实验证明了自己的结果。个人认为，主要可以学到关于模型的异质性和模型的反集中性两个特别有意思的性质。同时，我们也能够学习到一些数学上的表述，以及理论的证明思路。
本篇篇幅较长，难度较大，今天只更一篇（能力有限）