基本图灵机
定义和初始状态
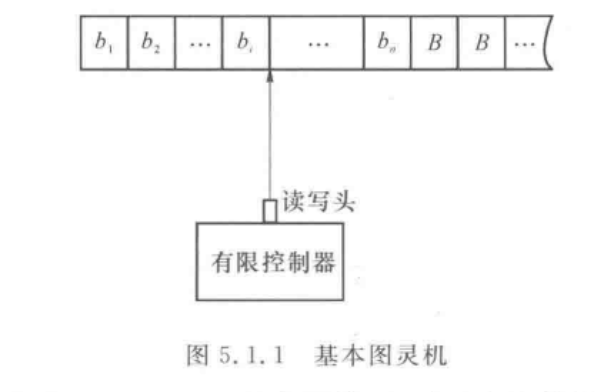
图灵机可以看作是具有一个读写头和输入带的模型。读写头每次读入一个单元的数据,然后决定是否写入,且读头左移或者右移。如下图所示:
形式定义
图灵机M是一个七元组,
- Q为有限状态集合
- T是输入字符集合
-
- B是空白符号
-
- F是终止状态集合
-
图灵机的瞬时格局
其中
示例:
图灵机不停的计算,直到进入接受状态或者拒绝状态(未定义转换函数)的时候中止。
设计简单的图灵机
采用图灵机进行字符串的读入
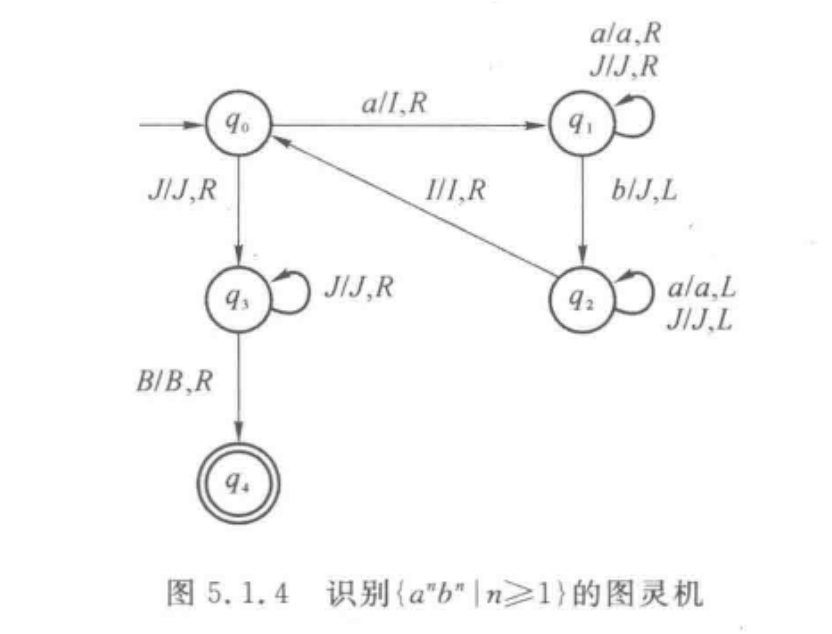
设上下文无关语言
仔细想想,由于图灵机具备相当强大的记忆能力,我们便可以将每个a,对应上一个b,只要最后完全对应上,那么就可以接受了,如果不能完全对应上,就说明出问题了。
具体流程如下:
-
图灵机从最左端开始,此时状态为q0,向右直到读入一个a,将其改写为I。
- 读入a之后,进入状态q1,右移直到找到b
- 将b改写为J,进入状态q2,左移直到找到I
- 找到I之后,进入状态q0,右移直到找到a,然后将其改写为I
- 重复以上过程
-
如果a被提前找完,那么在q0状态向右移动寻找a的时候,将不会寻找到a,此时如果读入b了,那么拒绝。如果没有找到b,而是找到了空白符,那么接受。
- 如果b被提前找完,那么在q1状态下,会遇到空白符,此时拒绝。
状态机如图所示
采用图灵机做整数到整数到函数计算器

如题所述,我们可以先读入m,然后读入一个n,1作为中间标记,如果m提前被读完,那么进入接受状态,接受0。如果n被提前读完,那么就记录剩余的m的个数即可。但是,由于本题给出了输入带上只能有0,1,B,那么我们可以用1来做右边的标记,用B来做左边已读入的标记。具体操作如下:
- q0状态起始,先读入最左侧的第一个0,将其改写为B,进入q1状态
- q1状态不停右移,直到碰到1,进入q2状态
- q2状态右移直到碰到0,改为1后进入状态q3
- q3状态左移直到碰到B,然后切换回q0状态
- 重复以上即可
- 对于接受状态,我们需要分两种情况讨论。
- (1)
- (2)
我们设置一个新的状态q5,当q2状态碰到B之后,我们无论遇到0和1都向左,直到碰到B为止。碰到B之后将B改为0,进入接受状态q6。
复杂图灵机
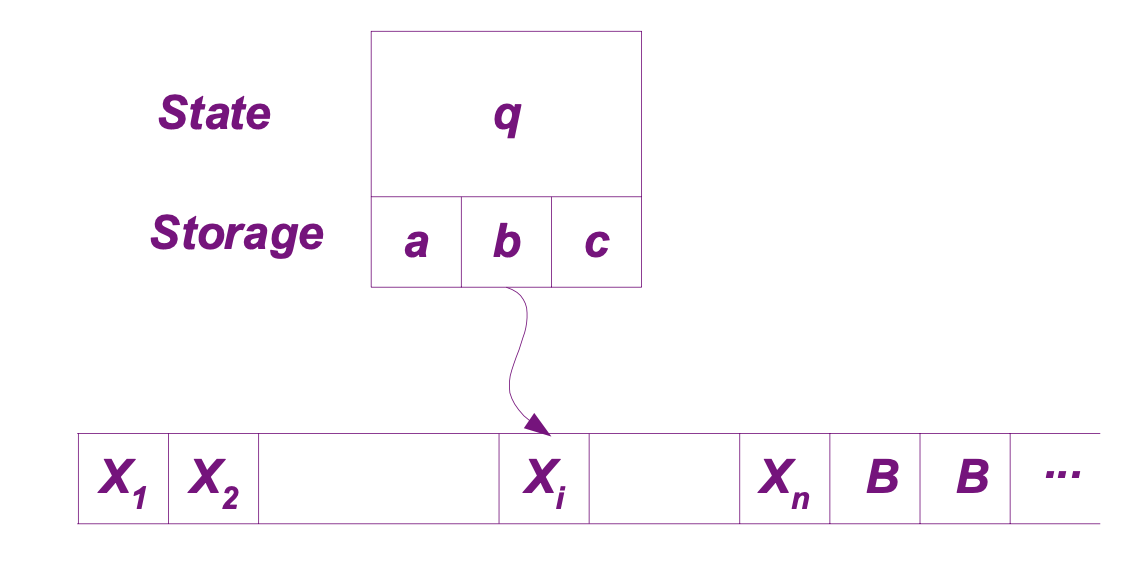
可存储的图灵机
我们可以设计具有存储功能的图灵机,使得它能够在读取的时候存储。我们将存储的功能集成到状态中,即将有限的状态变化为:
设计示例

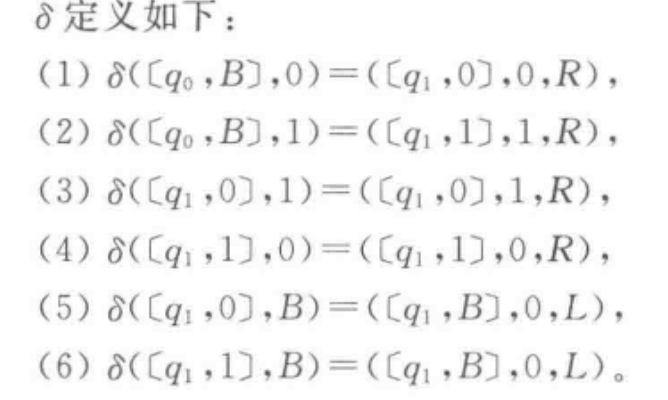
大概就是,如果遇到了和第一个相同的,就接受,反之如果走到B都没有,那就不接受。
如果遇到相同的,那么未定义,直接停机。
多道机
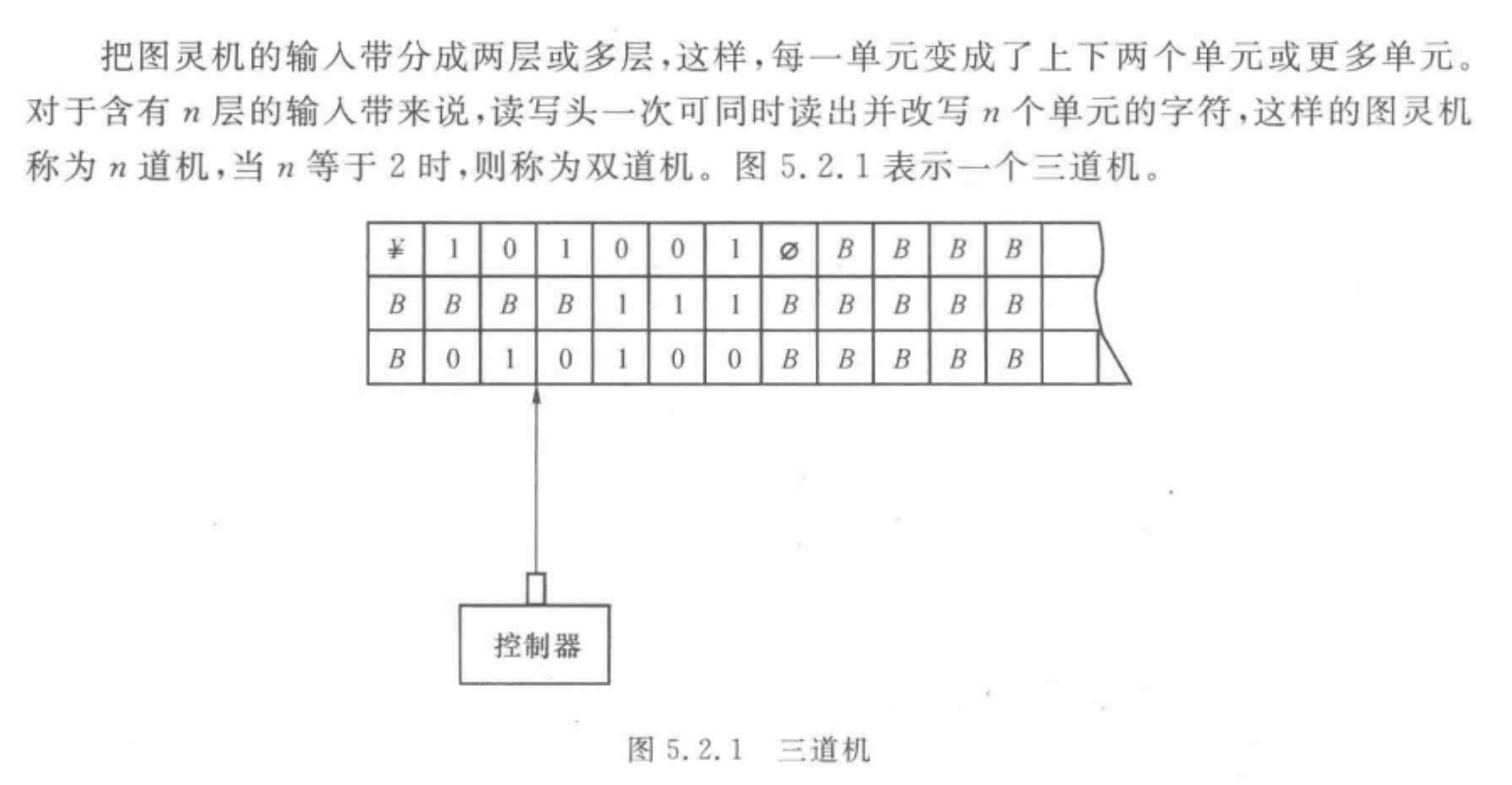
多道机设计示例

这个比较复杂,应该考的可能性很低,不过也做简单的说明。
大概就是,第一道放被除数,第二道放除数。第一道减第二道的结果放在第三道,一直反复减,直到第三道小于第一道。如果余数为0,说明非质数,如果余数不为0,那么它不可以整除第二道的数,因此我们将第二道的数+1,然后继续重复,直到第二道的数字等于第一道的数字为止。
核对符
类似于对表格打勾一样。我们一般可以转门增加一个道来核对对应的符号是否被“打勾”。
比如,对于识别
移位
可以让图灵机具有对字符串的移位功能。对于n位的移位,需要图灵机能够存储n位的数据。
示例:构造图灵机M,使得它将输入带上⾮空⽩字符向右移动两个单元。那么就需要能够存储2位的数据。
那么我们可以:
- 记录前两位的数据,然后进入状态q1
- q1状态下,每次拿取并写入存储的数据。
- 直到碰到B,那么进入状态q2,将存储的数据存入B中。
- 完成
如果您喜欢我的文章,可以考虑打赏以支持我继续创作.




