LoRA的原理理解

Motivation

对于正常的一个训练流程，为了让大模型更好的适配下游任务，我们需要进行二次训练。二次训练的过程中，我们需要对每一层的参数矩阵进行求导，然后进行梯度下降反向传播的方法，来更新其权重，本质是极大似然估计。但是，鉴于现在的预训练模型越来越大，动辄百亿乃至千亿的参数，让个人用户以及小公司直接对大模型进行二次训练时不现实的。其算力成本过大。因此，就有了LoRA这样的微调技术的出现

Procedure

我们知道，正常的二次训练的更新的流程为：
那么，二次训练的难点就在于，这个实在是太难算了。那么有没有办法处理掉它呢？
有的兄弟，有的。我们先设
我们可以这样考虑。对于初始模型的权重，我们在训练完之后他会变成，那么，我们的目的就是让，由于是通过最小化loss来得到的，那么，对于增量，我们可以把它视作一个可学习的参数，让它能够最小化loss就可以了！
LoRA的中心思想就出现了：参数化，冻结，最后使得得到的能够近似就可以了

但是，好奇的同学就会说了，那你这个参数化的，它形状岂不是和一样，那这样根本没减少计算复杂度啊！
诶~这里就是LoRA的第二个trick了，我们知道，微调数据集的数据量往往远小于预训练的数据集，因此，其实它对于的更新程度也是有限的，因此，我们只需要很少的信息量，来更新就可以了。这里LoRA采用的trick是利用矩阵分解技术，将分解为矩阵，通过A，我们可以映射到低维空间，B会将他映射回高维空间。这样我们就可以在低维空间进行训练，然后再把它映射回高维空间。
但是要注意，虽然形式上映射回了高维空间，但是其信息量和在低维空间是一致的，因此，这样的训练确实减少了参数，但是并不能等价于直接训练的效果。它也确实丢失了一部分信息~

下面上图：

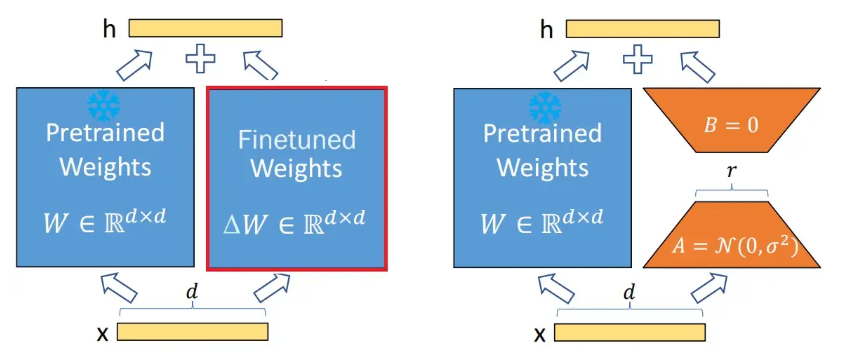
左边是直接二次训练的图，右侧是LoRA的图。
(这里还有一个小小的trick，为了使训练的初始状态和原模型一样，我们要让，但是，如果此时两个矩阵全为0，那么训练就无法开始了，因为对这两个求导都会是0，陷入鞍点出不去了，因此，初始化模型的时候会让B为0，而A从高斯分布采样)

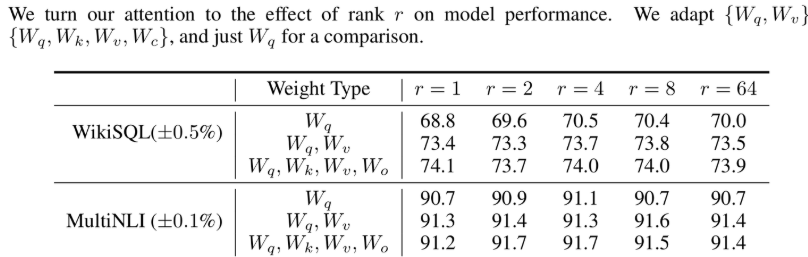
关于超参数r的选取

我们知道了，LoRA的本质，就是把增量矩阵参数化，然后映射到低维空间进行学习。那么，映射到的空间维数越低，丢失的信息就越多，同样训练起来的算力需求也就越低。映射到的空间维数越高，获取的信息就越多，当然同样也更容易过拟合（r不是越高越好），因此，需要平衡r的选择。这里论文作者给出了他的实验结果