PDA

基本概念与形式定义

对于PDA而言，其对应的表达能力和上下文无关语法一致。相比于DFA来说，它具有一定“记忆”能力，能够记住以前输入的字符。

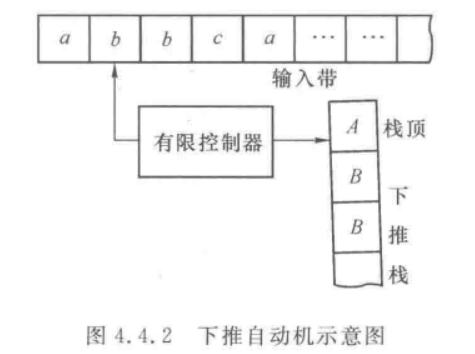
形式定义：不确定的下推自动机（NPDA）是一个七元组，其中，的定义和DFA一致
:即为其下推栈字母表的集合
:其下推栈的起始字符，
:转换函数，从到的映射
对于转换式
可以理解为是：在状态q，输入a，下推栈栈顶为Z时，切换到状态p，下推栈栈顶切换为

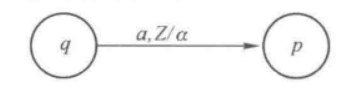
可以用以上的图形表示
若，则意味着栈顶被弹出

格局

下推自动机的瞬时工作状况，也可以用格局描述，是一个三元组，即，其中：
q:当前状态，
w:待输入的字符串，，当时，代表输入字符已经读完
a: 下推栈中的所有内容，，当时，代表下推栈已弹空
转换函数

可以用格局表示为：|——

构造PDA

构造PDA有两个核心，即其接收的方式。由于PDA的记忆性完全来自于栈的特性，因此，大部分的设计都是基于空栈标识的，即当栈弹空之后，就接收。
另外的一种接收方式是基于终态的，即设置一个终止状态，只要转移到终态之后，待输入的字符为空了，那么就接收
例1. 构造PDA，接收语言

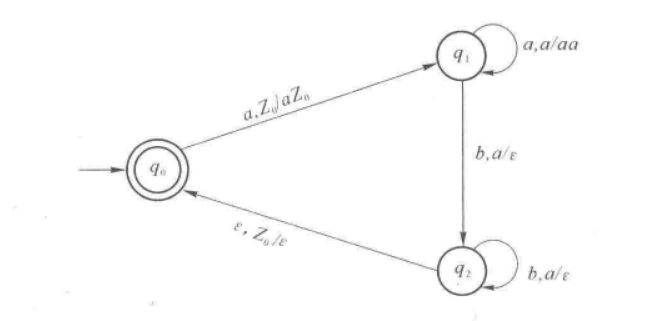
另外，我们还可以给出一个定理，来证明空栈接受和终态接受的等价性

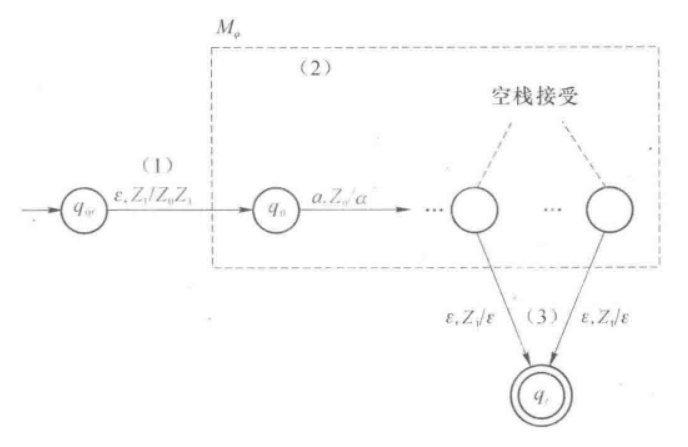
其主要思想就是，对于任意一个空栈接受的自动机，我们都可以将其空栈状态指向一个新的作为终结态。

上下文无关文法和下推自动机

由文法产生自动机

即，给定，G是一个上下文无关文法，则必然存在一个下推自动机接受
算法过程描述如下：
1) 将文法的起始符号S放入栈中
2) 重复以下步骤：
3) 如果栈顶是非终结符A，那么从A的生成式中随机选择一个，丢入栈中
4) 如果栈顶是终结符a，那么弹出并读入下一个符号，如果匹配，那么回到(2)，如果不匹配，那么这个非确定分支被拒绝
5) 如果栈空，且此时输入已经读完，那么接收这个字符串

算法的形式定义如下：
设，其中：
，，，，
的定义如下：
- 如果，那么含有
- 对所有，

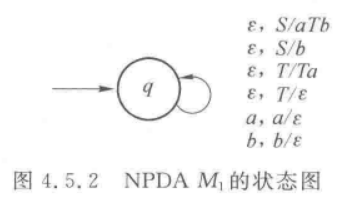
由自动机产生文法

即，给定一个PDA M，我们需要找到一个文法，它能够接受所有能够达到PDA接收状态的输入的字符。
先给出一个特殊的定义，代表一个非终结符，它的意思是，从q状态开始，对栈顶Z进行分析后，能够到达状态p，其意味着下面这个式子

w即输入的串
算法过程描述如下：
1) 构造起始生成式，其中p是下推自动机的所有状态。
2) 然后，从生成式中取一条来看，这里假设取出的是
3) 那么我们可以得知，从a状态，若此时栈顶为A，则可以消耗掉字符串w，并到达状态b，栈顶变为AZ，那么就可以建立生成式如下：
4) 对于空缺，每一个空都需要遍历所有的可能，不过，首尾需要呼应上才行，即第二个空需要和第三个空一致，Z后面的那个需要和第一个空一致
5) 不断这样遍历下去，直到所有的生成式都被搞定