运算方法与运算器

进制转换问题

二进制、十六进制和八进制的互化

首先，无论处理几进制转几进制，第一步都是把它分为整数部分和小数部分。
对于整数部分，如果是二进制转八进制，那么以三个数字为一组，如果是二进制转十六进制，那么以四个数字为一组，计算出数字直接按顺序抄下即可。
对于小数部分，也是同样的方法，以三个数字为一组或四个数字为一组，计算结果之后抄下即可。

十进制转化任意进制

整数部分：除以基数，然后取余得到最低位，逐步得到次低位，一直到最高位
小数部分：乘以基数，整数部分为最高位。然后再取小数部分继续乘以基数。一直到最低位。如果无法停止，那么就是无限的小数

定点数

定点数的编码表示

所谓定点数，指的就是小数点的位置是固定的数。这样的数一般在当代计算机中呈现为无符号整型和有符号整型这两种。
不过在计组中，我们考虑的范围稍微广一点
(1)定点整数
(2)纯小数（定点小数）
所以实际上，定点数的意义在于，人为的约定一个小数点的位置，采取默认的方式进行运算。

原码表示

最高位表示符号，其余位表示数的绝对值

补码表示

正数的补码和原码相同
负数的补码可以理解为是符号位之外，每个位反转之后再在最低位+1的结果
（其实也可以理解为是正数连带符号位一起，所有位反转之后再+1的结果）

反码表示

不重要，就是每个位取反

移码表示

主要在浮点数的阶码中使用。主要用于表示整数。
一般就是在真值X上加一个的常数值，一般用于把补码的负数部分给映射到正数域上。

C语言的类型转换方法

有符号数和无符号数的转换

有符号数和无符号数这种字长相同的数据，==我们不改变他们在内存中的储存方式，只改变我们解释这些位的方式==
举个例子，对于short类型的-4321，我们按照有符号打印出的结果是-4321，按照无符号打印出的结果是61215，他们的二进制表示都是1110111100011111

不同字长的数的互相转化（short，int）

大字长变量向小字长变量转换：将高位部分直接阶段，低位部分直接赋值（即使有符号也是这样）
小字长向大字长变量转换：分为两种情况，如果是有符号数，那么进行符号位拓展，如果是无符号数，进行零拓展

运算部件

一位全加器

全加器是CPU中最基本的加法单元，由加数，加数，低位的进位共三个输入，有本位和向高位的进位两个输出，其逻辑表达式如下所示：


真值表如下所示

0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
1	0	1	0	1
0	1	1	0	1
1	1	1	1	1

串行加法器

将上式中的每一个加法单元的进位输出和高位的低位进位串行链接。就实现了的结果

并行加法器及其原理

上式中

我们注意到，这里的是可以通过加上自身的不断迭代算出来的，因此，实际上我们可以不断对展开，直到展开到为止。
我们可以令，令
然后如此往下迭代
就得到
就得到了并行加法器的运算的式子

标志位和溢出

OF：判断有符号数是否溢出，本质是看符号位和运算是否出现异常，比如明明是加法，却从正数变负数，明明是负数减正数，结果却是一个正数。这两个情况都说明溢出了
CF(carry flag)：判断无符号数是否溢出，本质是看有没有对高一位（最高位之外的位）产生进位
ZF：标记结果是否为0
SF(sign flag)：标记结构的正负性

定点数的运算

移位运算

1、逻辑移位
直接硬移位，什么都不管
2、算术移位
对于右移的情况，低位移出，高位补符号位

加减运算

对于加减运算，一般都是用补码来实现的，减法就用加上它的补码来做运算。
要点：
1、符号位和数值位一起参与运算，得到的结果的符号位直接在运算中得出
2、运算结果也是补码
溢出结果判断：
如果用一位符号位来判断的话，规则就是，两个操作数的符号相同，但是结果与原操作数的符号不同，就说明溢出。
还有一种双符号法，即采用两个符号位做运算，如果出现两个符号位上的数不同的情况，则说明溢出。

乘除运算

乘法运算

对于定点数的乘法运算，主要分为两步
1、求符号位：由两个乘数的符号位异或得到
2、求解数值：利用竖式的方式手算即可。不过，一般教材中默认的都是给出纯小数作为定点数的运算实例，而非整数。所以按照小数的方式来运算就可以了。

除法运算

和乘法一样，也是通过竖式的方式手算，同样是符号位和数值位分开考虑
当然，要先填n个0（n是除数的长度）来保证长度

浮点数

让小数点的位置根据需要移动

浮点数的表示

一般地，浮点数可以表示为以下这个形式

其中，S填入0或1，用于决定符号位，M是一个二进制定点小数，称为尾数，用原码表示，R是基数，一般是约定好的，E是二进制定点整数，称为阶码，用移码表示。

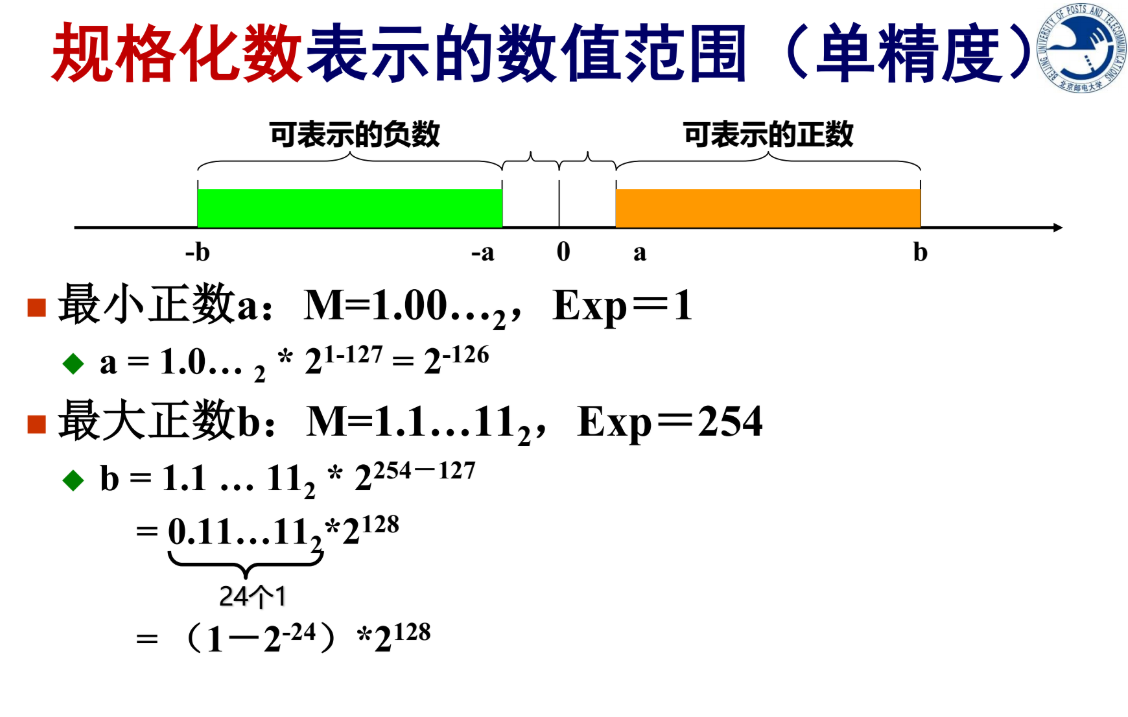
浮点数的表示范围

注意，这个表示范围这里==很重要==，如果阶码是补码表示，那么负数域和正数域将不再对称，要格外留心
特别说明：
对于正上溢：其临界状态为为全1并且阶码也全1
对于正下溢：其临界状态为：全0但最后一位为1，阶码为最小的

浮点数的规格化

总而言之就是通过修改阶码，让尾数最终移动到小数点右边刚刚好一个的位置。小数点前为符号位
例子：
1101.01011101 经过规格化得到-> 0.110101011101


注意，这里书上没有说，但是实际上，IEEE754的规格化和普通的规格化是不同的，需要格外注意

浮点数的运算

加减法

分为四步，第一步阶数对齐，第二步对尾数做运算，第三步对尾数进行规格化，第四步进行舍入操作
阶数对齐：小阶向大阶看齐
小阶右移阶差次，得到对齐的结果
然后对尾数进行加减运算
最后，在运算之后，我们大概率要进行舍入
舍入的方式分为四种

乘除法

和加减法类似，先对阶码做加减法
然后对尾数进行乘法/除法的操作
然后把结果规格化，再进行舍入
最后确定符号即可