第七章 参数估计

参数估计主要分为两大块内容，一部分是矩估计，一部分是极大似然估计

矩估计

其实很容易，就是把最后得到的期望矩和样本矩相等，就得到了参数的估计
一般来说，有k个未知参数的随机变量的分布需要求其1~k阶的原点矩（为了构建k个方程）
实际上，一般在考试中只需要求其期望，最多再加一个方差就够了。
举一个简单的例子：以泊松分布为例，假设，由于，所以我们知道，参数的估计值就是

极大似然估计

其实本质就是通过求似然函数的最大值时的参数的取值。
那么似然函数是什么，其实就是该总体事件发生的概率，只不过由于其分布函数中有参数，所以似然函数中含有相应的参数。
当然，对于连续性变量，求其每个独立事件的概率的乘积有些困难，所以数学家们通过证明，将连续性变量的似然函数表示为了其概率密度函数的乘积。
即：

这个就是我们的似然函数了。
那么我们对其求导取导数为0的点，就很容易得到其极值了
那么加上一点小技巧，由于连乘是不好算的，我们可以对其求对数在求导，这样可以把乘法转化为加法。这样就好求了。我们管这种函数叫做对数似然函数。

估计值的评选

1、无偏性：估计值的期望为其真实值
2、有效性：方差最小
3、相合性：会收敛(大数定律有用)

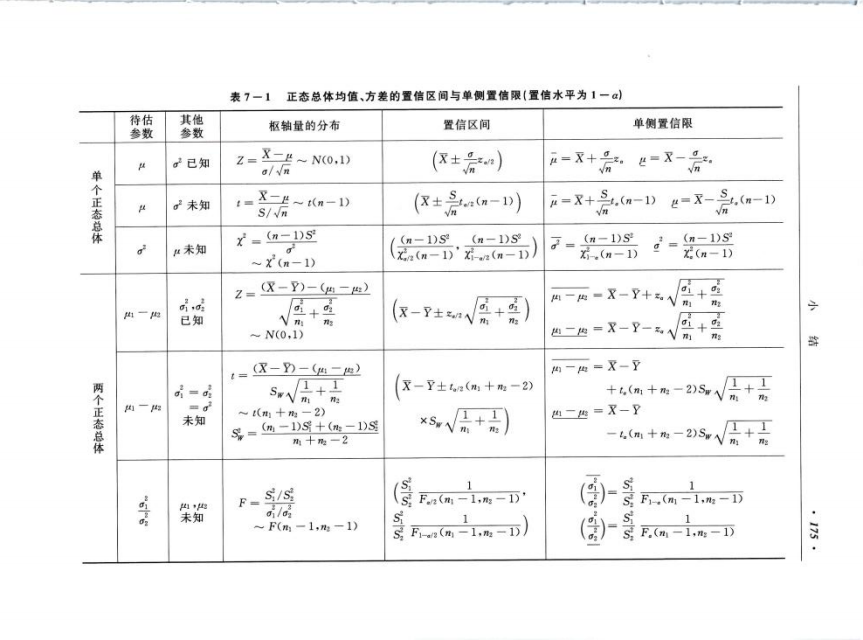
置信区间

这应该是本章最重要的一点内容了吧，学会了这个基本上下一章的假设检验也就问题不大了。

（想了解思想的可以看本段，不想看的可略过）对于本章，我们只需要知道，想要计算某个参数在给定置信度下的区间，我们必须通过随机变量来计算相应的概率。但是，随机变量的分布是未知的，因此，我们只能通过中心极限定理中的正态分布来估计。但是，对于多数情况，其真实方差是未知的，因此我们就用到了上一章的t分布和f分布。这种思想称作构造枢轴量法

如果只是为了应付考试，请死记以下表格，即可拿到本题分数

图片描述