有限状态自动机

DFA

DFA的形式定义：
其中，Q是有限状态集合
T是有限的输入字母表
是状态转移函数，是QT到Q的映射
是初始状态
F是终止状态集合
其中，可拓展定义到字符串级别
表示状态q，输入字符串w达到的状态
以后所有拓展过的状态转移函数，输入为字符串的，默认记作

NFA

和DFA相比，只是转换函数有所不同，它允许QT到的映射

子集构造法 NFA-DFA

如何将NFA转化为DFA？
可以预想到这在期中肯定是一个必考点

先从NFA的作为起始状态开始遍历。基础的遍历一遍状态转移表，记录其中的所有的状态。
将其中的状态作为接续转移表的起始状态，然后根据原表，求并集得到新的状态表
遍历反复，直到记录的所有状态都出现在起始状态集合中。

以例题为例

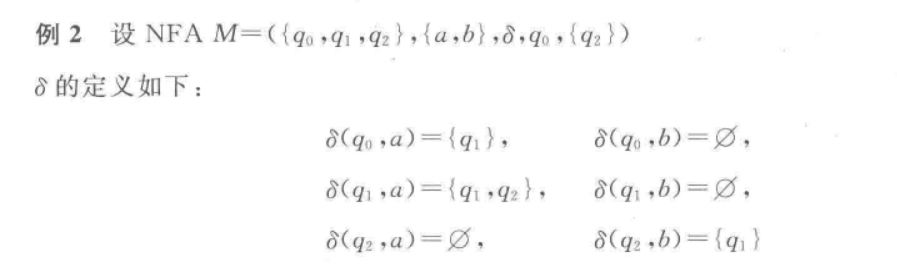
得到结果：

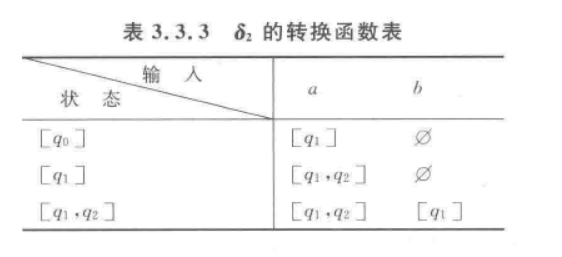
这种NFA具有一种特殊的能力，即同一时刻，即使无输入，他可能处于多个不同的状态。相比于NFA，它更加的“无条件”了一些。

那么显然，他天然的具有一个功能，即一个状态可以代表多个状态。这话有些绕， 但是我想说明白的是，通过连接的状态，在到达任意一个的时候，也意味着到达了其他的相邻的状态。
为了更清晰的描述这些状态，我们做出如下的定义
对于已知状态q，仅用转换便可到达的状态集合P，即为所求，记作

到NFA的转换

其实本质上，这种转换方式很好理解
我们需要明确一个前提：一个含有的NFA中，通过输入a，可以到达的点分为两种，一种是直接到达的，一种是和到达的点通过连起来的，因此，实际上我们可以把NFA中的转换函数表示为

也就是到达的点的闭包
但是，这还不算完全，因为，它的出发点也分为两种。一种是q，另一种是q通过可以直接到达的状态，即
综上，我们得到转换函数：

我们对所有的(q,a)对遍历以上算法，即得结果